集群分析用於將類似的族群群聚在一起,以下將詳細說明其原理及SPSS操作。
一、使用狀況:
集群分析是一種精簡資料的方法,依據樣本之間的共同屬性,將比較相似的樣本聚集在一起,形成集群(cluster)。通常以距離作為分類的依據,相對距離愈近,相似程度愈高,分群之後可以使得群內差異小、群間差異大。
*【小常識】
判別分析V.S.集群分析:
判別分析→將事先已分類好的觀察值,選取有分類效果的樣本,求出其判別函
數,再將觀察值進行適當分類。
集群分析→不需事先將觀察值分類,直接以觀察值的屬性進行分析。
二、分析方式:
集群分析不需要任何的前提假設,不過大致可分為以下三種分析方法:
(一)階層式集群分析法(Hierarchical method)
1、凝聚分層法(Agglomerative):開始時,每一個體為一群,將距離最近的兩個個體合成一群,一步步地使群組越變越少,最後所有的個體結合成一群。
依不同群間距離計算方式,又可分為以下五種方法:
(a) 單一聯結法(Single Linkage,又稱「最近法」)
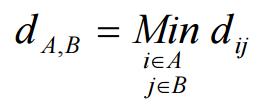
(b) 完全聯結法(Complete Linkage,又稱「最遠法」)
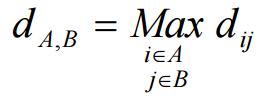
(c) 平均法(Average Linkage)
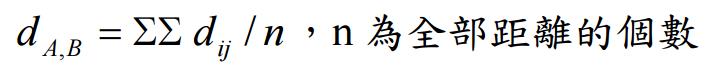
(d) 中心法(Centroid Method)
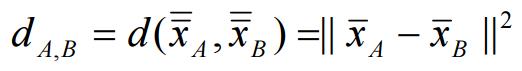
(e) 華德法(Wards Method,又稱「華德最小變異法」)
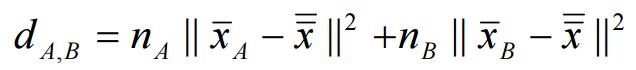
2、分離分層法(Divisive):先將所有個體視為同一個群體,再將相異性較大的個體一步步分成兩群、三群,直到每個體為一群。(此法不常用)
(二)非階層式集群分析法(Non-hierarchical method)
將原有的集群打散,並重新形成新的集群。
如:K平均數集群分析法
(1) 選定K個初始集群的中心,其中K是欲分群的數目。
(2) 計算每個觀察值到各集群中心的距離遠近,將每一個觀察值分配到離其最近的集群內。
(3) 根據事先假定的調整規則,重新分配每一個觀察值到K組集群中。
(4) 如果重新分配的資料點能滿足調整規則條件,則重複步驟(2)、(3),直到資料點無法重新配置為止。
(三)兩階段法
第一階段以階層式集群分析法分群,決定集群個數,第二階段再以K平均數集群分析法移動各群集內的個體,保持全部集群為k群為止。一般最常使用的是兩階段法,本文也將以兩階段法作為下述範例的操作。
三、SPSS 操作Example:
【例題】依據全班同學的體適能測驗結果,做體能差異的分群。
(一) 第一階段採用階層式集群分析法
1. 在SPSS中輸入欲分析之資料,變數包含座號、仰臥起坐、坐姿體前彎、立定跳遠的成績。
2. 階層式集群分析:分析→分類→階層叢集分析法
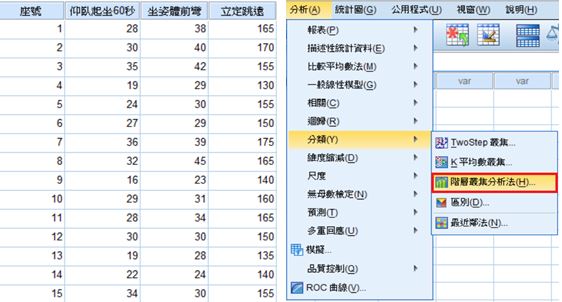
3. 變數→仰臥起坐60秒、坐姿體前彎、立定跳遠
觀察值標籤依據→座號
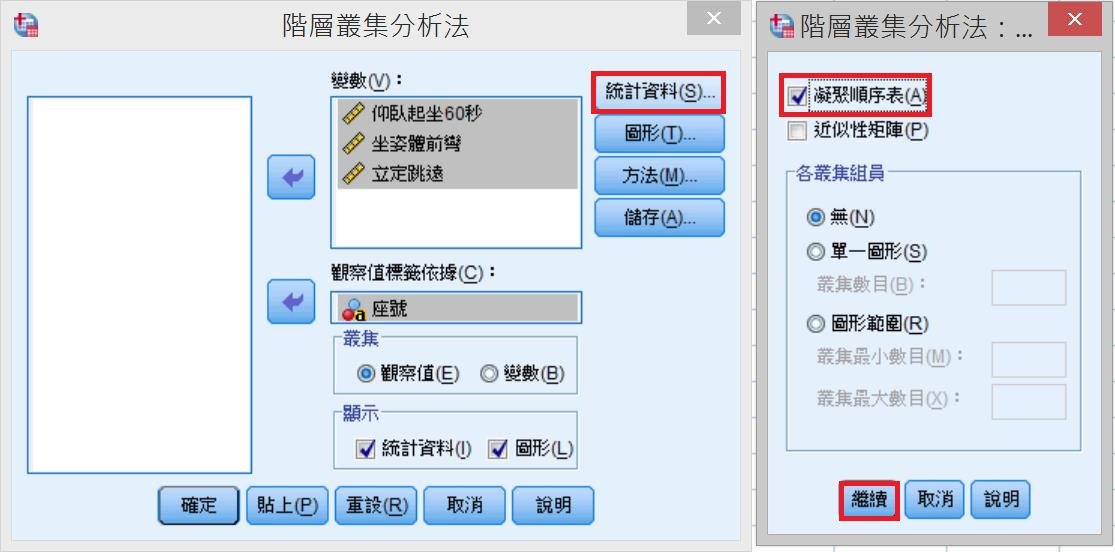
4. 統計資料→凝聚順序表
圖形→樹狀圖
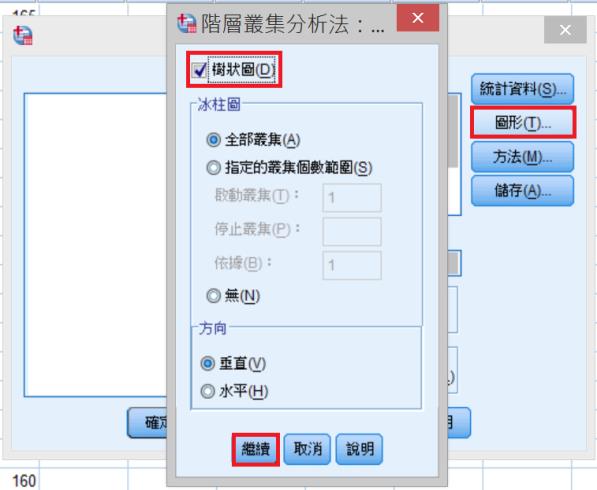
方法→叢集方法:Ward’s方法;區間:歐基里得直線距離平方
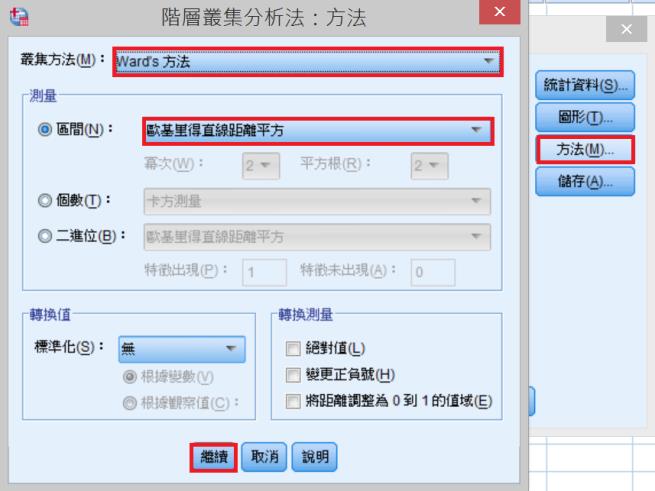
5. 輸出結果
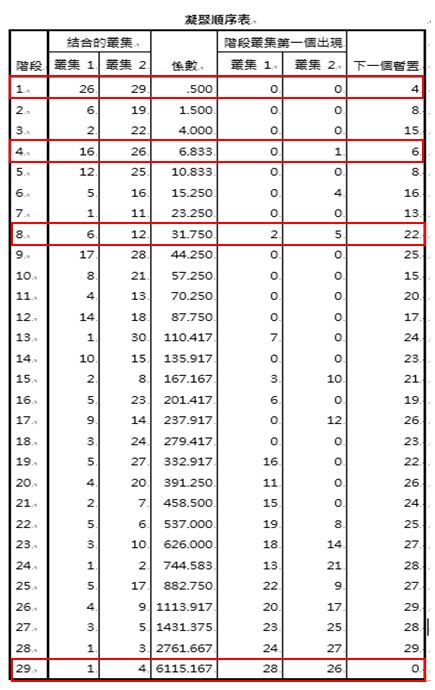
(1) 凝聚過程說明:
(a) 階段一時,座號26與座號29合併形成「類一」,先出現的階段集群
(0,0) 表示樣本與樣本之間的合併。
(b) 接著在階段四時,座號16與座號26所在的「類一」合併,先出現的階
段集群(0,1)表示樣本與類一的合併。
(c) 在階段八時,先出現的階段集群(2,5)表示類二與類五的合併,也就是座
號6、19和座號12、25合併。
(d) 最後一階段時,所有的學生將合併成一群。
*【小常識】
凝聚順序表中的係數為距離測度值,值愈大表示兩者之間差異愈大,當係數突然增大許多則不宜再合併。
(2) 樹狀圖:
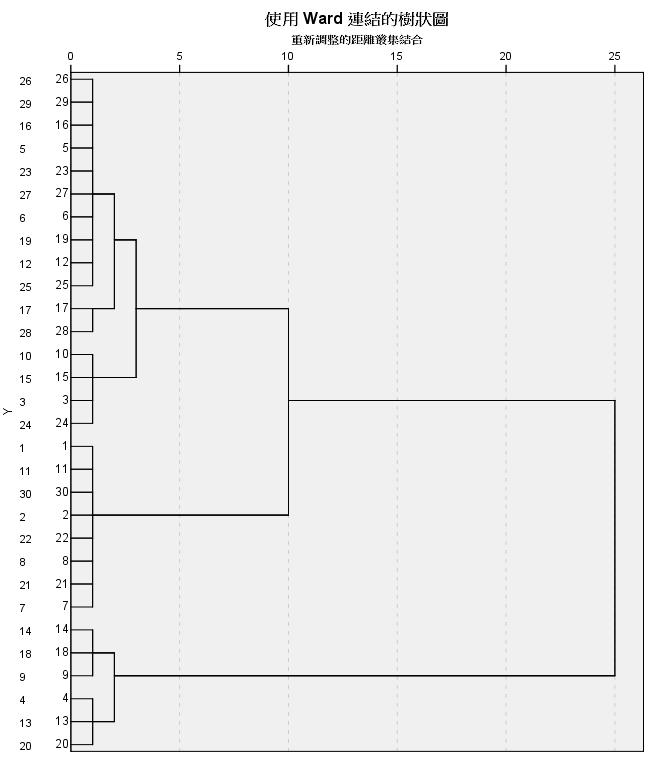
→由樹狀圖可以看出分成三個集群較為理想,接著進行第二階段。
(二) 第二階段採用K平均數集群分析法
1. K平均數集群分析:分析→分類→K平均數叢集分析法
2. 變數→仰臥起坐60秒、坐姿體前彎、立定跳遠
觀察值標籤依據→座號
3. 叢集個數:3
以階層式集群分析法的樹狀圖中,得知最佳分群數為三群。
4. 選項→各叢集初始的中心、ANOVA摘要表、各觀察值的叢集資訊
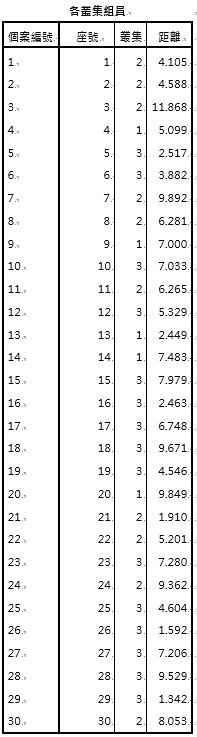
5. 儲存→各叢集組員
6. 輸出結果
(1) 在原始資料的末端會出現一欄新變數,表示集群分析之分群結果。
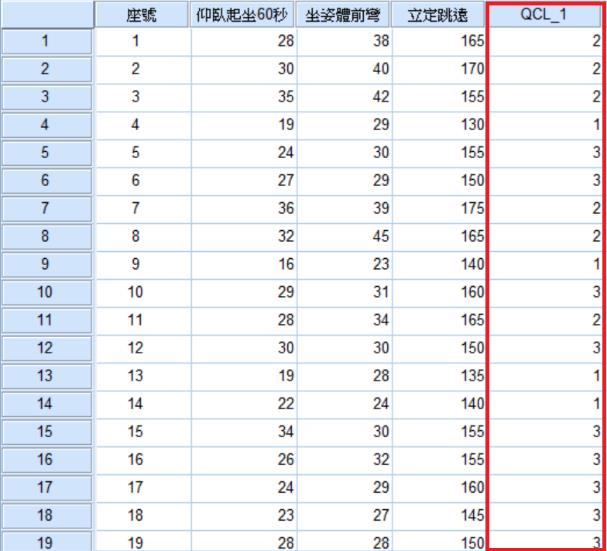
(2) 各叢集組員顯示出每個同學的集群代號及其與該集群中心的距離
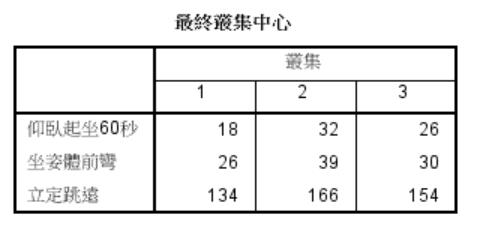
(3) 最終叢集中心可以顯示各集群的中心點性質,可依據此表格為各集群命名。
在本例中,集群二在三種體適能檢測中的表現都是最優異的,我們可將集群二命名為「金牌組」;而集群三在各項表現居中,可命名為「銀牌組」;集群一則在各項檢測的表現都最差,可命名為「銅牌組」。
(4) 分別以三個不同檢測項目為依變數、集群別為自變數進行變異數分析,F值都相當顯著,表示分群結果還算恰當。



封面圖-500x383.png)


