驗證性因素分析是結構方程模型中的一個環節,用於探討觀察指標與潛在變數之間的關係,以下將詳細說明其原理。
一、使用情形與說明
結構方程模型(SEM)基本上由兩個部分所構成,一是測量模型(measurementmodel),另一個則是結構模型(structuralmodel)。本次要探討的觀念與實作就是測量模型的部分:也就是觀察指標與潛在變數間的關係,一般我們是以驗證性因素分析(CFA)來處理這方面的分析。
跟醫科學所關注與測量的變數幾乎皆為可觀察的變數(例如血壓或體脂肪)不同,在行為科學,尤其是心理學,政治或社會學等領域,常常會要測量一些比較抽象的概念。舉例而言,心理學家可能想測量個體的「自我效能感」(self-efficacy)。但這個構念人人都在談,卻人人沒見過,因為其本身較為抽象。這時候,心理學家就想fit了一種方法:藉由測量許多關於自我效能感的行為、認知或態度等相對可明確表徵的指標,從中來萃取並架構該抽象構念存在的合理性。這種方法就稱為因素分析。
二、理論介紹
(一)因素分析
因素分析分為兩種,一為探索性因素分析(EFA),一則為驗證性因素分析(CFA)。探索性因素分析(EFA)多為發展或編製量表時所用,用來理解那些指標(題目)該被選入或刪除,以及一個構念(潛在變數)底下分別具有那些向度(或可稱為分量表)等。驗證性因素分析(CFA)則多用於一個量表發展完以後,用以檢驗是否特定的指標(題目)都歸到理論預期的各向度底下,主要的目的是理論驗證。
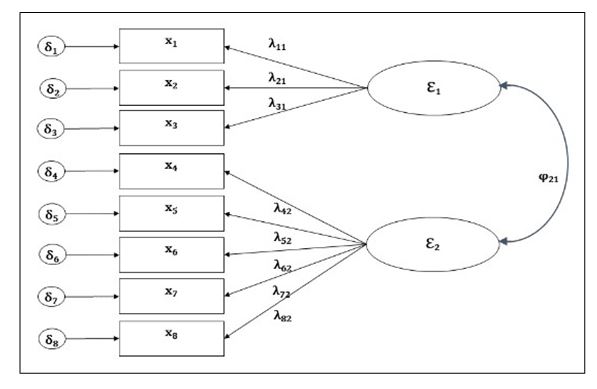
舉例而言,如果研究者開發了一個量表測量「工作倫理」該潛在變數,而依照EFA的結果,其下又可分為工作態度與工作意義感兩個向度,並且分別有X1~X3,以及X4~X6這六題分別在該兩向度底下。那麼我們在進行CFA時,就會依照理論設定模型,然後看整個數據適配的結果如何?簡言之,就是看理論與實證數據是否貼近,以為驗證。典型的驗證性因素分析(在SEM中或稱為測量模型)如下例圖:
(二)信度分析
此外,在古典測量理論中,有所謂信度(reliability)的概念,簡單來說,我們利用量表或測驗測得的分 數可以拆解為兩個部分:圖中的E1與E2分別代表兩個潛在變數(構念),其下分別被X1-X3,以及X4-X8這些可觀察的指標(observedindicator)所測量。而λ則是因素負荷量(factorloading),絕對值介於0-1之間,表示該指標與特定潛在變數之間的關聯強度,其平方則表示「潛在變數能解釋該觀察指標變異的百分比」。
根據Hair等人(2006)的觀點,λ大於等於.71時,就算是一個相當理想的指標,而一個指標(題目)的因素負荷量至少要大於等於.55,才算是可以接受的一個標準,在那數值以下的題目可能就不算很理想,需要予以斟酌。但這些判準並沒有這麼強硬,端賴於各個科學領域對於測量的品質需求到甚麼程度。一個量表呈現的公式為:
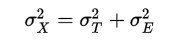
公式中下標為X的的變異數為觀察分數,而下標為T的部分為真分數,而下標E的部分則為誤差分數。由於許多的測量或多或少都有誤差,故將真實分數的變異最大化,或將誤差分數的變異最小化就是測量的理想目標。這代表著我們真正測量到我們所測量的構念的比例是愈高的,而其他不相干的因素所佔的比例是相對愈低的。信度的公式也非常直觀,就是1(總變異)減去誤差分數的變異部份:
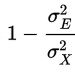
(三)結構方程模型
在結構方程模型(SEM)中,也有學者(Fornell&Larker,1981)提出類似的概念。
組合信度(compositereliability,CR),計算公式如下:
(factorloading的總和)*2/((factorloading的總和)*2+殘差變異數之和)
可以上面該公式理解到,組合信度意味著這些觀察指標的總變異可以被該潛在變數所以解釋的比例究竟有多高。而該兩名學者(1981)也提了平均變異萃取量(average variance extracted, AVE)此一量數,公式跟組合信度很類似,但差別在於AVE是將factor loading先各自平方後,再加總起來。一般而言AVE大於.50時,測量模型的表現算相當理想。稍微介紹完測量模型(或是驗證性因素分析)後,接著看看如何在R 語言中實地執行這個分析:
三、R程式範例
(一)安裝與載入
首先,我們先安裝lavaan這個模組(package),lavaan是latentvariableanalysis的縮寫,這是由比利時GhentUniversity的YvesRosseel教授所撰寫的模組。

Rlanguage中每個模組,如剛剛下載的lavaan安裝後,每次重新啟動R,都得用函數library()將其載入後才能使用:

成功載入後,我們可以先利用lavaan內建的一個範例檔:HolzingerSwineford1939來做分析,首先用函數names()來查詢該數據檔有哪些變數?

數據檔內有9個測量指標(X1-X9),都是測量mentalability,根據理論內有三個潛在變數,分別是visual,textual跟speed三個factor的心智能力。
(二) 模型建模
上圖中的語法為R language中,測量模型建立的方式。”=~”意味著”measured by”,該符號左側是潛在變數(構念),右邊則是該潛在變數底下的測量指標,因為一個構念絕大多數都是用複數的測量指標來測量,在R language中,我們用”+”號將其連接起來。注意三個式子外面,我們各用一個撇將其包覆起來,並存入LV.model(名稱可自定)這個變數中:

接著,這些設定都完成後,進入重頭戲CFA的部分,在Rlanguage裡,我們會調用函數cfa()來進行這個分析,語法如下:

我們將CFA的分析結果存入model.fit這個變數(同樣的,這個變數名稱也是自訂的),接著再調用函數summary()來顯示詳細的分析結果:
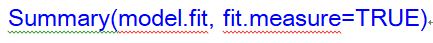
跑出來的報表如下:

第一張圖顯示了整個模型配適的狀況。舉例而言,CFI是一個愈高表示適配度愈好的指標,介於0-1之間,大於.90代表適配度不錯。右上橘色框為各個因素的factor loading,值得一提的是,研究者可以在函數cfa()內加上一個命令:std.lv=T,經標準化後,這樣就可以對每個觀察指標的factor loadings進行比較:
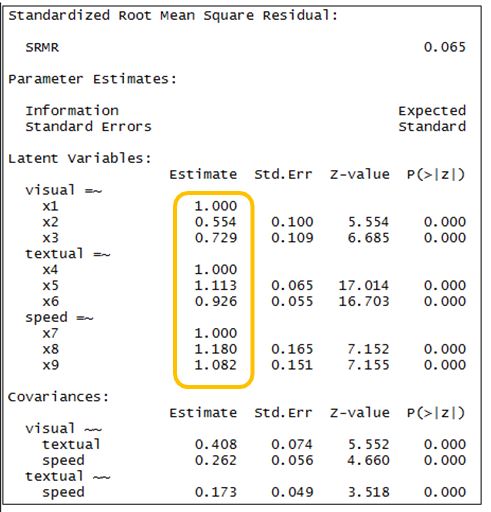
我們可以從最下面的variances觀察到,三個因素的變異數都為1。這顯示了std.lv=T該命令的效果,每個潛在變數的變異數都相同並等於1,而現在橘框內的各因素負荷量也可以進行比較,用以判斷變項的關聯性及影響力。
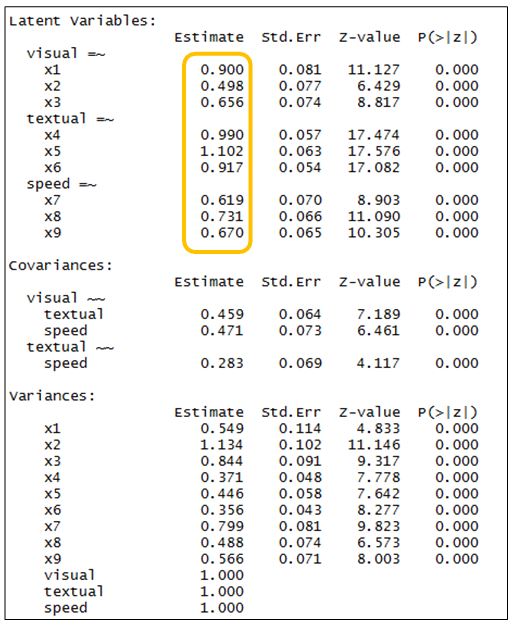
驗證性因素分析(CFA)就是結構方程模型(SEM)中測量模型的部分,它探討潛在變數(例如自我效能感或自主性等等)的組成與關係是否符合研究者的理論;基本上,待每個潛在變數的測量模型在統計上被驗證後,我們才會進一步探討各潛在變數間的「理論上的因果關係」,也就是結構模型的部分,兩者合起來就是我們之後會看到的結構方程模型。
值得注意的是,跟一些計量方法,尤其是近來很熱門的機器學習比較不同的是:
結構方程模型大體上是一種理論驗證的統計工具,這也是它被社會科學家喜愛的原因,因為其可以探討複雜的變數間的關係進而建構理論,控制測量誤差,以及比較不同的理論觀點間,何者跟實證數據比較配適?甚至美國著名的Deloitte consulting(勤業眾信)還曾經使用該方法來做HR analytics,以便增進組織的效能。結構方程模型還有各種延伸的模型,以便處理各種複雜的研究需求,基本上已成為各行為科學學門相當倚重的方法之一。


封面圖-500x383.png)


