在本篇文中我們將會簡單介紹存活分析中的Cox regression model(Cox proportional hazard model),用以分析會顯著影響死亡率的變數,以下詳細說明。
一、使用狀況
在過去的文章中,我們已經說明Life-table method的用途,以及Kaplan-Meier method與其檢定方式log-rank test跟 Wilcoxon test,這些方法都用於簡單的組別比較,屬於無母數的分析。
如果想要同時校正其他因素(干擾因子),我們可以使用有母數分析的預測方式,比較常見的是Cox proportional hazard model,此模型用於探討影響存活率的重要因子。
二、前提假設與理論說明
在探討Cox regression時,存活函數及風險函數這兩個部分要先釐清。
(一)存活函數 (Survival Function):
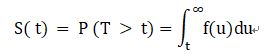
t 是時間點
S(0)= 1
S(∞) = 0
存活函數呈現的是在某特定時間點之下,個案可以活過特定時間點的機率是多少。
(二)風險函數 (Hazard Function):
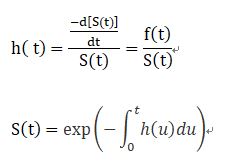
風險函數h(t)值不隨時間變動。
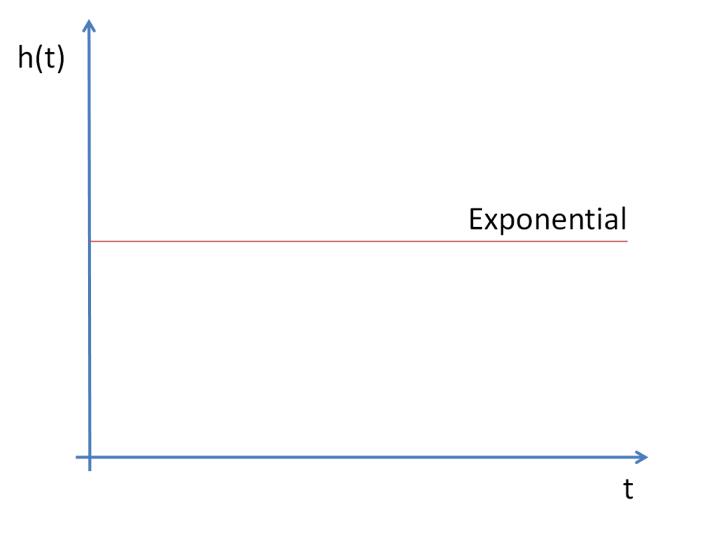
t 是時間點,風險函數h(t)值與存活時間有關。
舉例來說,如果t=3個月,h(t)就是事件機率(死亡)除以3個月時的生存函數。因為t越大,存活函數S(t)越小(存活函數為遞減函數),假定死亡機率密度f(t)對任何時間點一樣,那麼風險函數h(t)值越大,預期存活時間短。
在Cox proportional hazard model之下
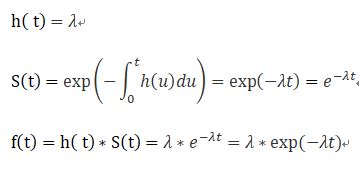
λ為一定值,由此可推導出Cox proportional hazard model為:
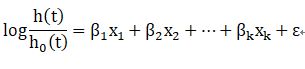
其Hazard Ratio計算方式如下:
假設今天只有一個變項x1,x1=1(treatment)跟x1=0(placebo),則風險比會如下:
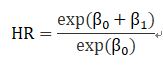
三、SPSS 操作Example
(一)在SPSS中輸入欲分析之資料。
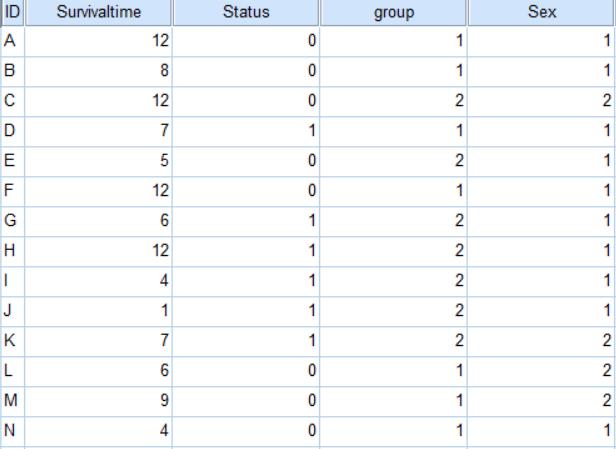
目前有14位分別使用不同藥物的兩組胰臟癌病人,我們追蹤了12個月,獲得他們到過世前存活時間的資料,我們利用這筆資料,分析胰臟癌的存活率。
Group表示治療組:第一組為新藥,第二組為舊藥;Sex表示性別:第一組為男性,第二組為女性。
(二)分析→存活分析→Cox回歸
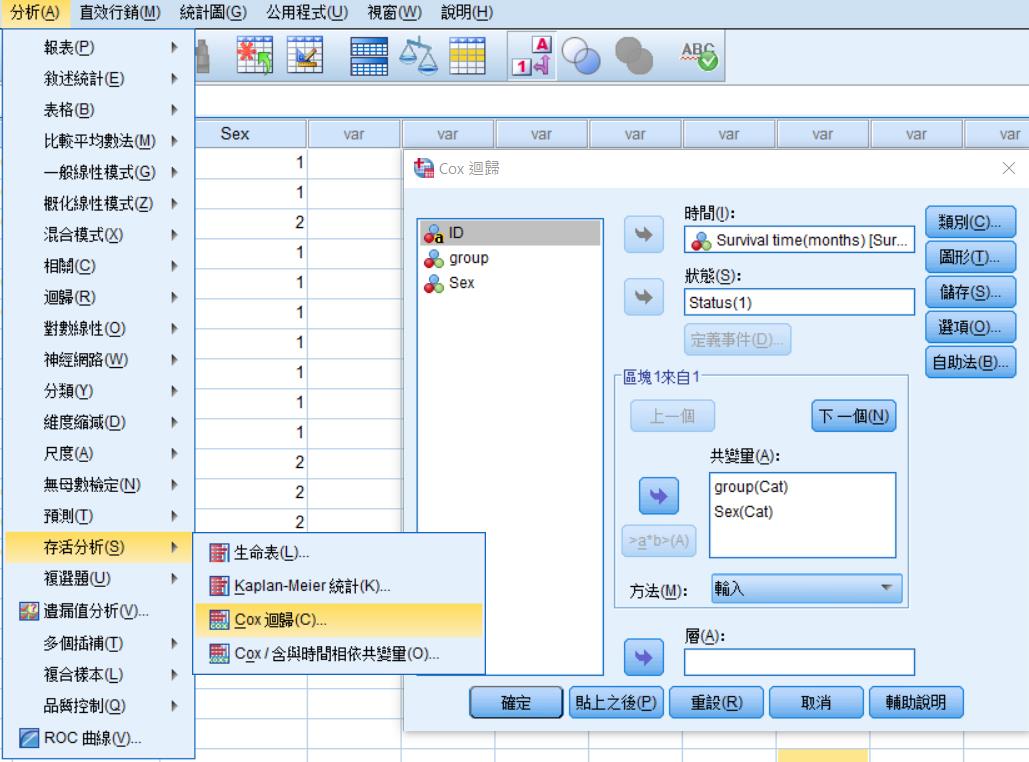
(三)Cox回歸
時間:點選Survival time。
狀態:選event的變項,定義事件要定義什麼樣的值為event,所以填1。
共變量:選變項group跟sex。
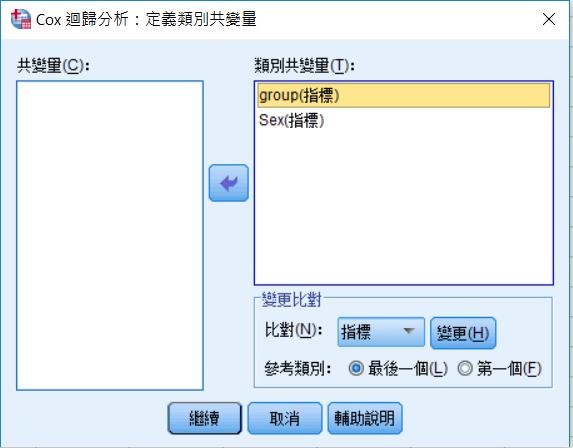
另外在右上角的「類別」裡把「共變量」的將group跟sex放入「類別共變量」並在比對選「指標」,「參考類別」看你想要以哪個為Reference group,我選最後一個是把舊藥當成參考。
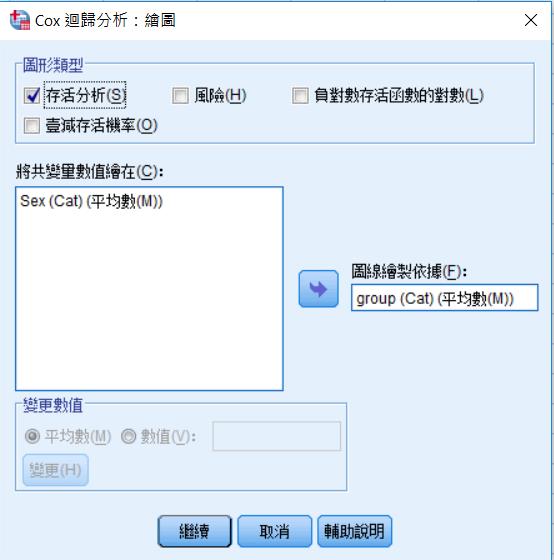
圖形裡面,勾選「存活分析」,「圖線繪製依據」選group
(四)結果:
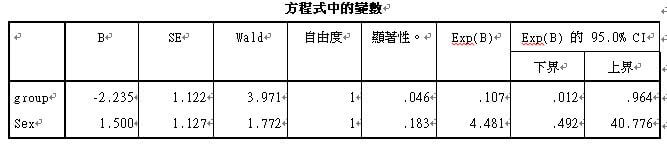
結果如上表,我們可將他整理如下:
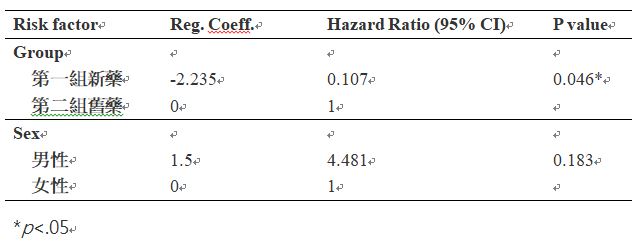
由上表可以看出,控制了性別之後,第一組新藥相較於第二組的舊藥的死亡風險比為0.107,且有達到顯著上的差異(p=0.046),但在性別上未達統計上顯著的差異(p=0.183)。由此可知,若控制住其他醫療或是個體差異,則新藥的效果顯著了降低了病人的死亡風險(實務分析中做這樣的推論則必須更為謹慎)。
(五)繪圖
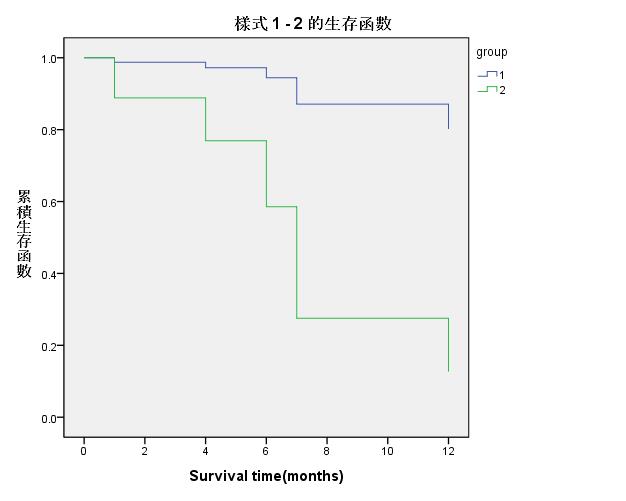
點選「圖形」就會輸出Kaplan-Meier法的生存函數圖,由此圖也可知第一組存活的時間較長,死亡數目較少。


封面圖-500x383.png)


