在做每一次的資料分析之前,我們首先要做的就是資料預處理,再來就是資料清洗,這相當重要。試想你手上的資料集合裡有很多的遺失值、離群值等等,那麼可想而知做出來的統計分析絕對不會太準確,而為了減少我們錯誤分析的結果,因此需要我們來整理、歸納甚至丟棄這些遺漏值、異常值。
一、處理遺漏值(Missing Value)
所謂的遺漏值,通常指的是資料某些不小心被刪失、截斷甚至有可能是忘了紀錄,種種因素導致我們資料有遺漏值,然而當資料量龐大時,遺漏值是非常常見的。而遺漏值存在時往往導致分析結果不準確,因此我們會希望透過一些方法來處理資料集合中的遺漏值問題。
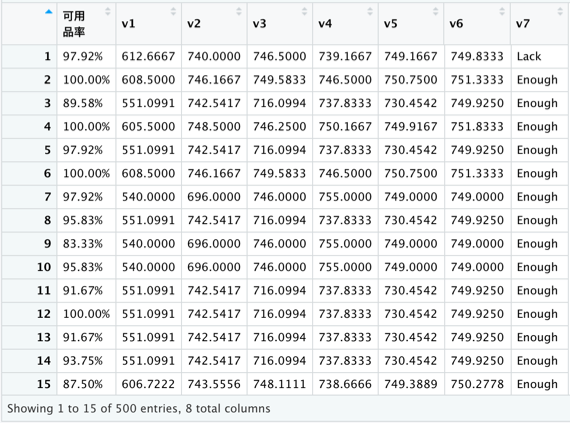
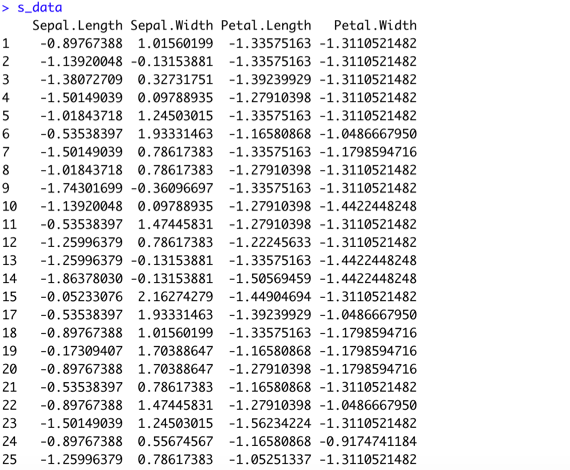
在R語言內,若有遺漏值存在,系統會在該缺失值用NA來做表示,看下圖示(紅色方框內數值即為遺漏值):
(一)檢視、計算遺漏值:檢視是否有遺漏值存在通常使用is.na()函式
#首先匯入一個製造業資料集合
m_data <- read.csv(“/Users/yutang/Desktop/manufacture.csv”)
#檢視整體資料遺漏值存在狀況(顯示前六項即可)
is.na(m_data)%>%
head()
#檢視整體資料是否存在遺漏值
anyNA(m_data)
使用is.na()函式後,若該筆資料是遺漏值時,會以TRUE表示,反之則會以FALSE表示,這樣可以清楚看到該資料是否具有遺漏值,或者可以以更快方式anyNA()函式來確認該資料集合是否存在遺漏值(一個以上及算存在)。
#計算整體資料遺漏值個數
is.na(m_data)%>%
sum()
#計算資料各欄(各變數)之遺漏值個數
is.na(m_data$v1)%>%
sum()
is.na(m_data$v4)%>%
sum()
#計算各個變數的遺漏值存在比例
sapply(m_data,function(df){sum(is.na(df)/nrow(m_data))})
(二)遺漏值填補:在檢測完是否存在遺漏值後,我們就要開始進行處理遺漏值問題了,而第一種處理遺漏值的問題就是將其填補上去,依據資料類型,如果是數值型通常會以平均數、中位數來進行填補,若資料是類別變數就以眾數進行填補。
#因該資料集合變數都是數值型態,就以平均數來進行插補
#針對變數1、3、5欄位進行插補,以該欄位平均數為插補值(計算平均數時以na.rm = T 忽略遺漏值)
m_data$v1[is.na(m_data$v1)]=mean(m_data$v1,na.rm = T)
m_data$v3[is.na(m_data$v3)]=mean(m_data$v3,na.rm = T)
m_data$v5[is.na(m_data$v5)]=mean(m_data$v5,na.rm = T)
#針對變數2、4、6欄位進行插補,以該欄位中位數為插補值(計算中位數時以na.rm = T 忽略遺漏值)
m_data$v2[is.na(m_data$v2)]=median(m_data$v2,na.rm = T)
m_data$v4[is.na(m_data$v4)]=median(m_data$v4,na.rm = T)
m_data$v6[is.na(m_data$v6)]=median(m_data$v6,na.rm = T)
#填補完後記得再次檢查遺漏值存在狀況
is.na(m_data$v1)%>% #0
sum()
is.na(m_data$v2)%>% #0
sum()
is.na(m_data$v3)%>% #0
sum()
is.na(m_data$v4)%>% #0
sum()
is.na(m_data$v5)%>% #0
sum()
is.na(m_data$v6)%>% #0
sum()
#因爲該資料集合沒有類別資料,因此先將變數七(v7)轉為類別變數型態
nm_data <- m_data %>%
mutate(v7 =if_else(v7 <=750.00, “Lack”, “Enough”)) %>%
mutate(v7 = as.factor(v7))
#查看一下是否調整完畢
nm_data$v7 %>%
head(50)
#接著我們以眾數來進行填補(先以sort()函數算出眾數)
M=sort(nm_data$v7,decreasing=T)
summary(M)
#發現Enough較多,以Enough進行填補
nm_data$v7[is.na(nm_data$v7)]=”Enough”
#最後再次檢查整體資料是否都已完成遺漏值填補
anyNA(nm_data) #FALSE
View(nm_data)
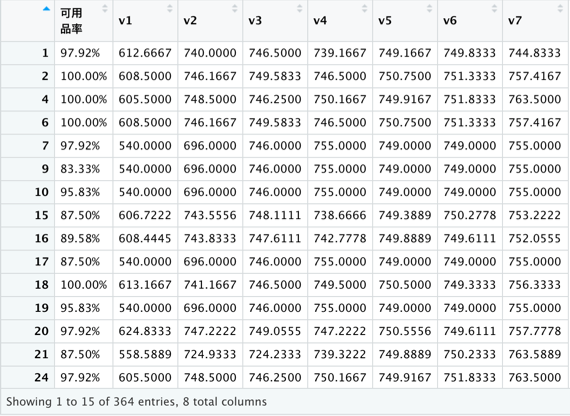
這樣就完整的填補了遺漏值囉!!!
(三)刪除遺漏值:通常不建議直接刪除遺漏值,因資料量(樣本數)太少也容易造成分析結果不準確,除非是遇到遺漏值太多使該筆資料能提供的資訊太少,我們才會考慮將其刪除,刪除遺漏值的方法很簡單,以下示範。
#刪除遺漏值
dm_data=na.omit(dm_data)
#刪除後,再次檢查遺漏值存在情況
anyNA(dm_data) #FALSE
View(dm_data)
這樣就刪除完成囉!!!
二、處理離群值、異常值(Outlier)
相信學過基礎統計學的同學們一定知道,若一資料集合含有不少離群值的話,往往會造成我們計算敘述統計量的時候有不精確的問題,或者當有離群值存在時,可能會導致我們所分析的結果產生難以解釋的情況,諸如此類的種種問題,無法讓我們忽視其存在,因此就讓我們正視問題並解決它。
1.標準化判斷法:
該方法也是利用到基礎統計學的概念,首先要先將所有資料轉換為標準化分數或Z分數,又根據常態分布的經驗法則,有 99.7%的觀測值落在母體平均值正負3個母體標準差的範圍內。因此若觀測值落在樣本平均值正負3個樣本標準差以外的數值,可判定該觀測值屬於離群值。
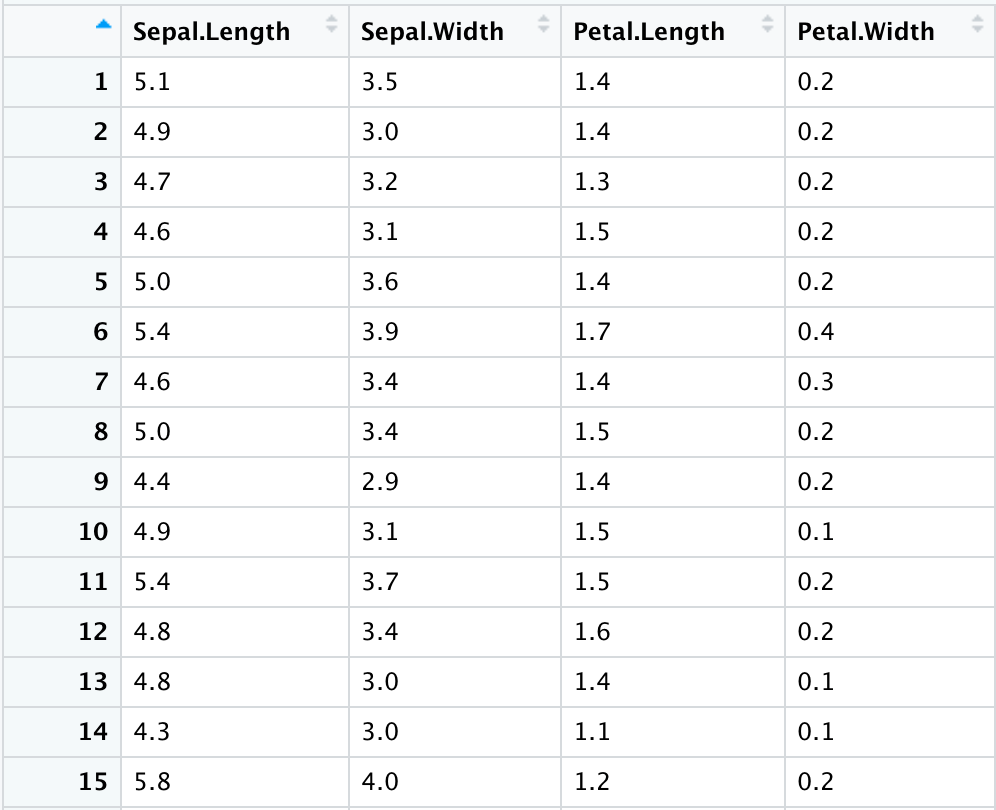
#我們使用R語言內建資料集合iris(鳶尾花)當作範例資料集合
data_sample <- iris
View(data_sample)
#可以稍微看一下該資料集合的資料結構以及其擁有的變數量和資料量,其中有一列變數不是數值型態(Species),我們將其移除(利用上章節教的分割資料)。
data_sample <- subset(data_sample, select= -Species)
View(data_sample)
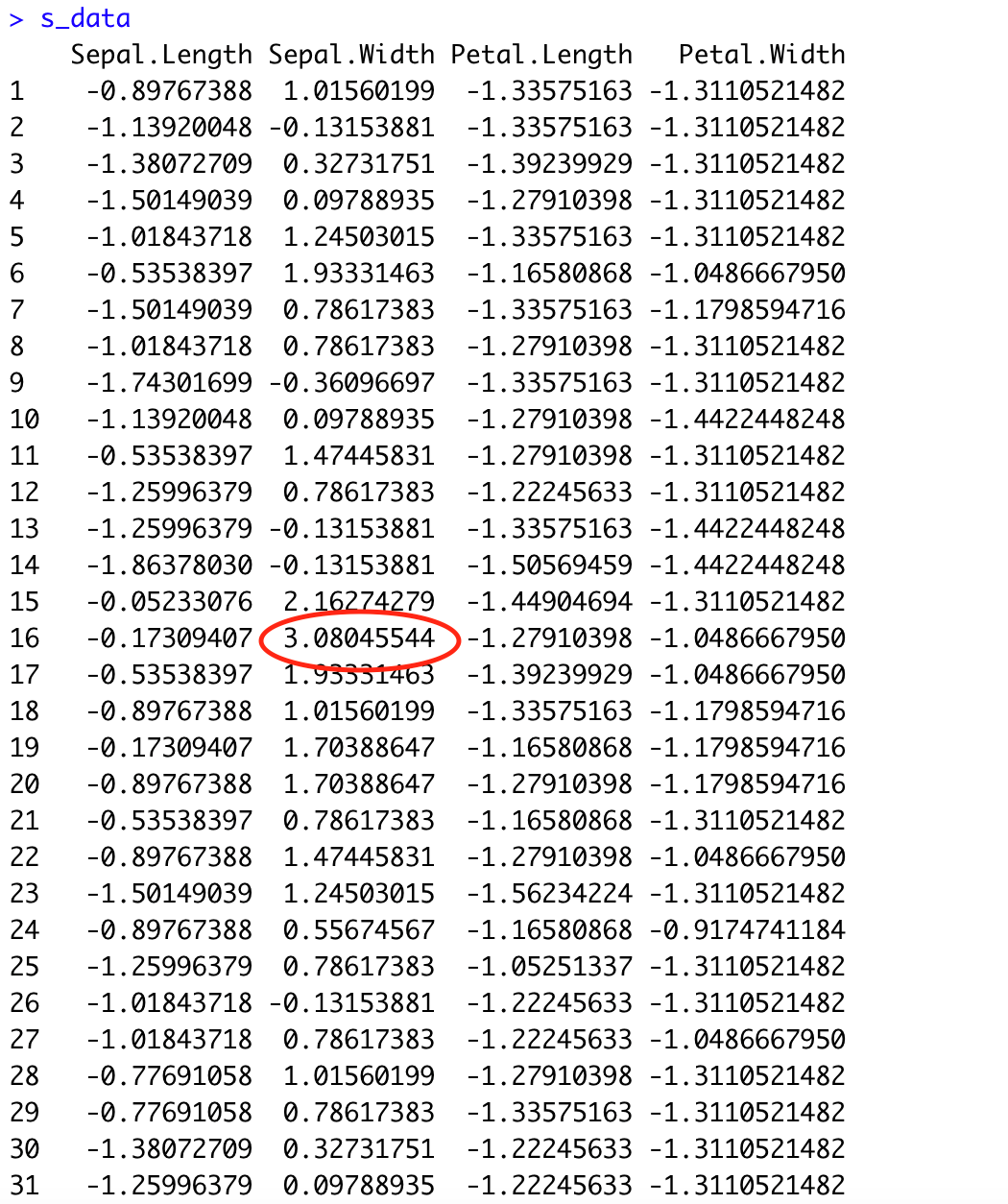
#接著使用scale()函式將我們資料集合內的數值全都標準化並且將其轉製成資料框
s_data <- data_sample %>%
scale(center = T, scale = T) %>%
as.data.frame()
#將分數 >3 和 <-3 之資料移除(留下介於兩者之間的資料)
s_data <- subset(s_data, Sepal.Length <3 & Sepal.Width <3 & Petal.Length <3 & Petal.Width <3)
s_data <- subset(s_data, Sepal.Length >-3 & Sepal.Width >-3 & Petal.Length >-3 & Petal.Width >-3)
#可以看到介於兩者之間的資料被保留下來
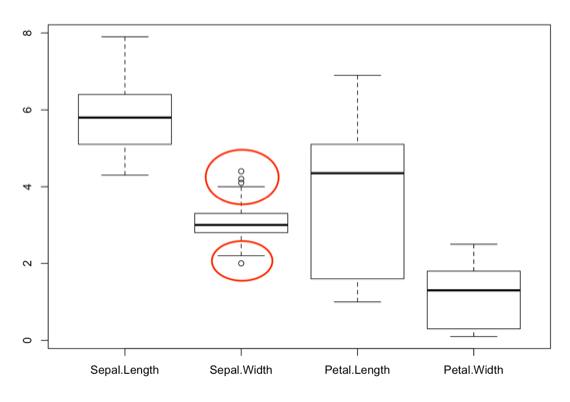
2.盒鬚圖判斷法:
盒鬚圖為顯示數據分佈情況的統計圖,它的組成有最大值、最小值、中位數、第一四分位數以及第三四分位數,而盒鬚圖中最重要的是決定籬笆 (fence),籬笆為第一四分位數−1.5×IQR與第三四分位數+1.5×IQR,而若有數值超出值籬笆範圍內,則被我們視為離群值。
#首先一樣要先將資料轉為資料框類型,接著用boxplot()函式將盒鬚圖繪製出來
s_data <- data_sample %>%
as.data.frame() %>%
boxplot()
#處理離群值時,先看離群值的數值落在何處以及確切數值為何
b_data$out
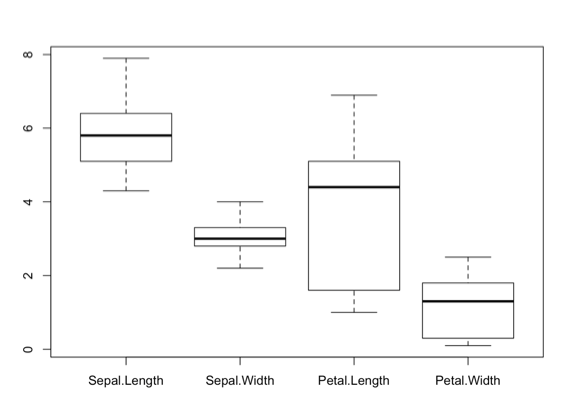
#接著將其剩餘數值切割出來(排除<2.0以及>4.1以上數值)
b_data <- subset(data_sample, Sepal.Width < 4.09 & Sepal.Width > 2.1)
boxplot(b_data)
總結以上離群值若是在可以解釋之範圍,那麼就可以不必移除它,但若離群值已經超出解釋範圍(特殊個案)並且影響分析結果時,就必須透過以上方法將其篩選出來。
*小結:以上就是資料清洗的過程教學,大家在拿到陌生資料集合時,碰到遺漏值、異常值的機率是非常高的,資料清洗的動作就尤其重要!在我們學習完並熟練資料清洗和資料預處理後,就可以開始進行統計分析、預測甚至建模等等…那麼就敬請期待後續教學內容囉~







封面圖-500x383.png)


