本文旨在介紹多元迴歸交互作用 – 差異中的差異法(difference in differences, DID)，以下說明其模型並利用Stata來分析範例資料檔。

 

一、模型說明

　　差異中的差異法通常用於分析政策或是其他外生刺激的效果 (例如：導入新的醫學療程對於病人健康狀況的影響，或是分析政府實施新的政策對於人民行為的改變)。首先將研究標的分成受政策影響的實驗組 (experimental group) 以及不受政策影響的控制組 (control group)，分別計算實驗組與控制組政策前後的差異，再將差異彼此相減，得出差異中的差異值，是為該政策的效果。

　　我們舉一個簡單的例子，假設小明擁有A、B兩塊相同性質的土地，且都栽種相同品種的樹木，此時友人告訴小明有一款新的生長劑，可以讓樹木生長速度加快，且只需噴灑一次之後就有效果。小明為了測試該生長劑的成效，在A土地的樹 (簡稱A樹) 灑生長劑 (是為實驗組)，而B土地的樹 (簡稱B樹) 不灑生長劑 (是為控制組)，其餘條件 (例如：澆水次數、澆水量與日照時數等) 皆維持不變。小明3月1日灑生長劑，並於9月1日檢驗效果，為了瞭解成效，我們列出3月1日與9月1日兩樹生長高度如下：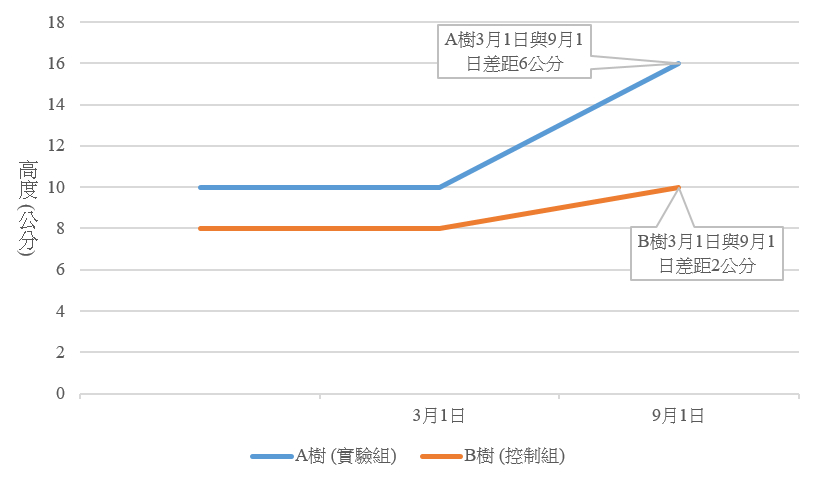

圖1 樹種生長高度圖形

 

表1 樹種生長高度表格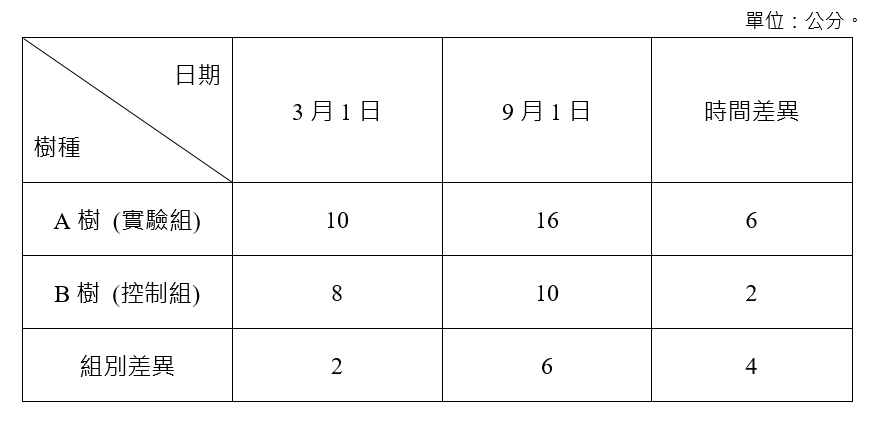

　　此時利用差異中的差異法，分別計算A樹與B樹噴灑生長劑前後的高度差異，分別為6公分與2公分，再將兩樹前後差異計算差異，為4公分，此為政策效果，代表生長劑確實有助於樹木生長。除此之外，也可先計算兩樹政策前與政策後的差距 (政策前3月1日兩樹差2公分，政策後9月1日兩樹差6公分)，再將政策前後的差異相減，結論依然相同。

　　此時有人可能會懷疑，為何需要控制組來凸顯政策效果，而非直接觀察噴灑生長劑的A樹生長成效即可，讓我們將上述生長成果的數值變化一下：

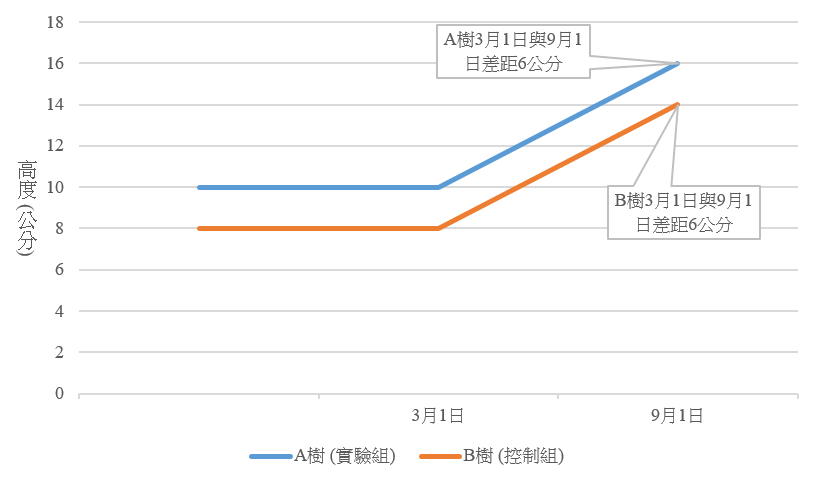
圖2 樹種生長高度圖形

 

表2 樹種生長高度表格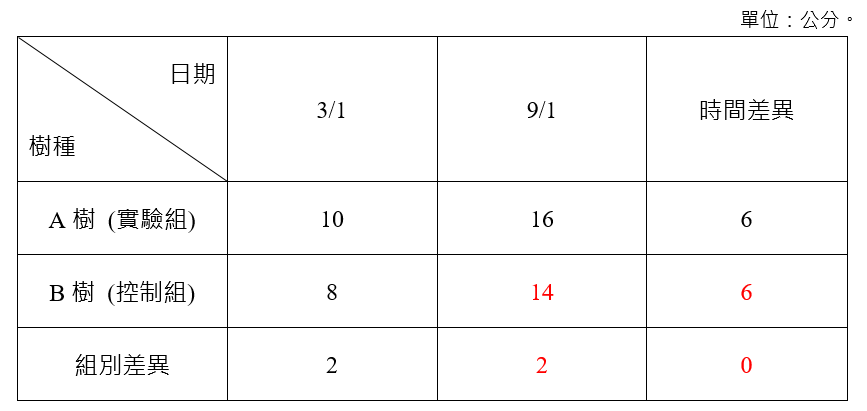

　　紅字代表有更改的部分，此時計算差異中的差異為0，代表生長劑無任何效果，如果只觀察A樹噴灑前後的差異 (6公分)，會誤以為該生長劑有效。其原因在於，影響樹木生長的變數很多，難以完全觀察到，表2的情況中，AB兩樹的成長速度一樣，可能是受到其他因素影響 (例如：樹本身的性質、日曬等)，如果只觀察A樹的結果，會忽視其他影響生長的因素對於A樹的影響。這也凸顯差異中的差異一個重要性質：一般來說，影響被解釋變數的因素非常多，無法完全觀察到，差異中的差異藉由控制組與實驗組的互相對照，可排除其他因素對於被解釋變數的影響，呈現我們想了解的政策效果。

 

二、計量模型

　　一般來說，差異中的差異的計量模型如下：

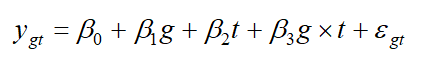
　　ygt為被解釋變數， g代表是否為實驗組的虛擬變數 (dummy variable)，是實驗組為1，否則為0；t代表時間是否為政策實施後的虛擬變數，如果該樣本是於政策實施後的時間，為1，否則為0，g × t為兩個虛擬變數的交乘項。差異中的差異模型中，g × t的係數β3是我們要觀察的政策效果，也就是差異中的差異，其原因藉由簡單的數學推導如下：

　　前面已經提過，差異中的差異是先分別計算實驗組與控制組政策前後的差異，再將兩個差異計算差異，寫成數學式即為：

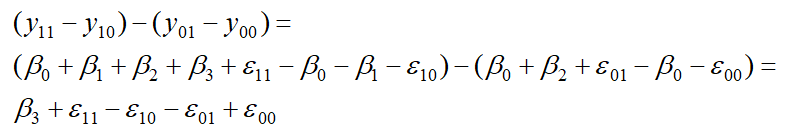
　　將差異中的差異取期望值為 (殘差項期望值為0)：

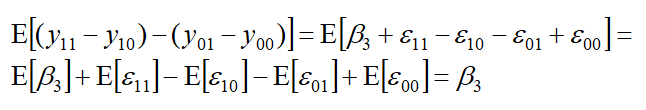
　　根據推導結果，差異中的差異值的期望值為β3，因此β3為我們欲觀察的政策效果。

　　然而，差異中的差異仍存在計量上的限制，由於需要計算政策前後的差距，因此必須假設政策前的趨勢 (trend) 相同，也就是說政策前任一時間點實驗組與對照組的差距須相同，否則政策效果會因為政策前時間點的選取不同，而有不同的結果。除此之外，政策本身必須為外生給定，也就是說政策施行與否並不受其他內生變數影響。

 

三、Stata操作範例

　　差異中的差異模型於Stata的操作上，僅須建立如同前述的迴歸式，再用最小平方法 (Ordinary Least Squares, OLS) 跑迴歸即可：

1. 在Stata輸入欲分析之資料：

　　範例檔共計1,200筆資料，group為是否為實驗組的虛擬變數，該變數為1代表為實驗組，反之為0；time為樣本是否於政策年度之後的虛擬變數，該變數為1代表於政策施行年度之後，反之為0；interaction為group與time的交乘項，y為被解釋變數，也就是政策影響的標的。

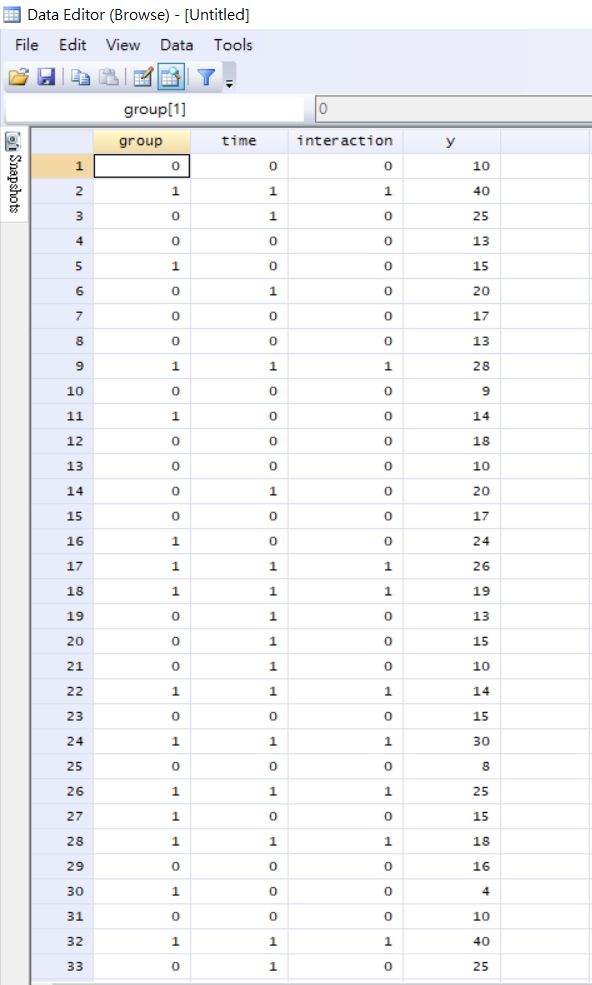
2. 建立迴歸模型：

　　迴歸模型為：

　　以最小平方法分析，Stata指令為 reg y group time interaction。

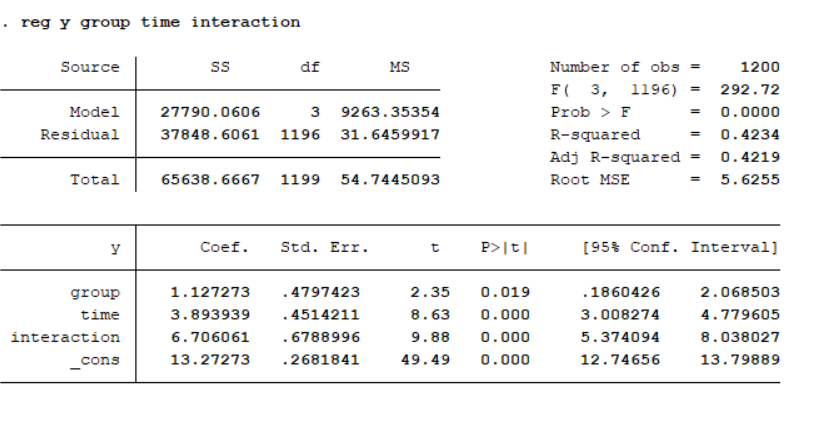　　_cons為常數項 (也就是迴歸式的β0)，代表迴歸式的截距項，也就是說所有樣本都具有的效果，不因個體變異而改變。

　　group代表政策施行之前 (time=0)，實驗組與控制組的差異，是為顯著正相關 (1%顯著水準)，代表沒有政策之前，實驗組對應的被解釋變數本身即超過控制組，該變數的意義在於，控制除了政策因素之外，剩餘影響實驗組與控制組差異的變數，其概念在於，如果只看政策後兩組的差距，政策之外其他影響兩組差距的變數會使我們誤判政策效果 (以表2例子來說，政策後實驗組與控制組差2公分，如果不看政策前會誤以為有效)。

　　time代表控制組 (group=0) 於政策實施前後的差異，是為顯著正相關 (1%顯著水準)，代表控制組於政策後其被解釋變數顯著增加，該變數的意義在於，控制所有除了我們欲探討的政策之外，剩餘於政策施行當下有所改變的因子，因為政策施行同時，可能會有許多無法觀察到的現象也於該時間點同時發生，必須消除其他隨時間變化的影響，以估計精確的政策效果。舉例來說，延伸前面提及的生長劑例子，如果3月1日噴灑當天，發生其他有利生長的情形 (例如：3月1日前天氣寒冷，而3月1日後天氣開始穩定且溫暖)，必須要控制該因素的影響，才能計算純粹的政策效果。

　　差異中的差異模型中最重要的變數，也就是我們最想知道的政策效果為變數interaction，該變數為差異中的差異計算結果 (先計算實驗組與控制組政策前後的差異，再將兩者差異相減，如同前面舉例所述)，如果為顯著正相關，代表政策實施後，確實提升實驗組的被解釋變數，政策有效。