當不滿足使用卡方檢定的條件時,可採用Yate’s correct test或Fisher’s Exact Test。
本篇文章主要介紹 Fisher’s Exact Test – R語言的操作,細節如下所述。
#補充:何時使用卡方檢定or 費雪爾正確概率檢定
當總樣本量大於40,最小期望次數大於5 =>卡方檢定;
當總樣本量小於40,最小期望次數小於5 =>費雪爾正確概率檢定(Fisher’s Exact Test)。
一、費雪爾正確概率檢定 (Fisher’s exact test)
這是一種用於2×2列聯表、行列的總數不超過20個、有細格期望值小於5的情況下所使用的無母數檢定法,可分析兩組類別資料之間是否有顯著相關。
(1) 資料形式:
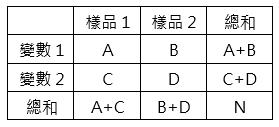
(2) 假設檢定:
H0:兩族群分佈相同
H1:兩族群分佈不同
(3) 費氏精確機率公式
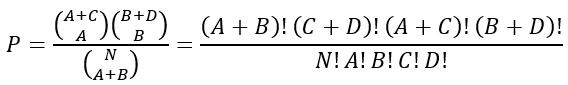
二、R語言操作範例
(一) 範例介紹
為研究西瓜工廠日班和晚班輪班工作者所生產不良品之比率是否相同,蒐集資料如下表:
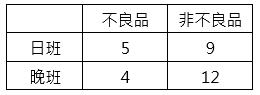
試以 α = 0.01為檢定之顯著水準,可得到何種理論。
(1) 設p1、p2分別表示日班、晚班所生產不良品之真正比率,其假設檢定為:
虛無假設→ H0:p1=p2。
對立假設→ H1:pi不全相同,i=1, 2。
(2) 顯著水準 α = 0.01
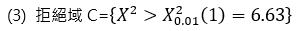
(二) 資料匯入
Work<-read.csv(“Work-2.csv”,header=T)
# read.csv ():將資料匯入到指定的變數,也就是Work
View(Work)
# View():瀏覽資料內容
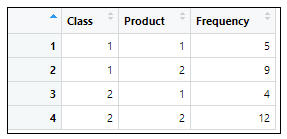
=>根據執行結果:在資料集中共有3個變數和4個觀察資料,3個變數分別為:
班別(Class):1: 日班、2: 晚班;商品(Product):1: 不良品、2: 非不良品;頻率(Frequency)。
(三) 統計描述
- 資料整理
data<-data.matrix(Work$Frequency) #取Frequency資料轉矩陣格式
rname<-c(“Day”,”Night”) #行名稱
cname<-c(“NonGood”,”Good”) #列名稱
compare<-matrix(data,nrow=2,ncol=2,dimnames=list(rname,cname)) #資料整理並編輯為矩陣格式
compare #查看數據

=>根據執行結果:列出了Fisher確切概率法所需要的資料格式,並存儲在「compare」資料框中
- 統計描述
S1<-prop.table(compare,margin = 1) #計算行百分比
S1 #顯示行百分比

=>根據執行結果:可知輪班工作者生產不良品之比率分別為:日班0.36%、晚班0.25%
S2<-chisq.test(compare,correct = TRUE) #進行連續性校正
S2$expected #查看期望次數

=>根據執行結果:可知日班、晚班的期望次數;其中在不良品的部分,期望次數均<5。
# 補充:在卡方檢定中,一般要求期望次數不得小於1,並且不得有20%以上細格的期望次數小於5。
不然則建議合併相鄰的行或列,或採用Yate’ s correct test,或採用Fisher’ s Exact Test。
- 統計推斷
fisher.test(compare) # Fisher確切概率法
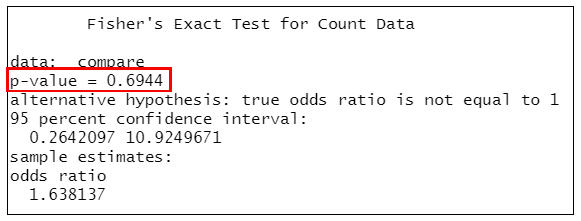
=>根據執行結果:列出p值、對立假設、95%信賴區間、勝算比(OR值)。
因P=0.6944>0.01,可知兩班輪班工作者所生產不良品之比率為無顯著的差異。
三、結論
本研究採用費雪爾正確概率檢定(Fisher’s exact test)對日班和晚班輪班工作者所生產不良品之比率是否相同而進行分析,由於總樣本量(30)<40,應使用Fisher’s exact test 進行分析。根據分析結果顯示,日班不良品之比率為0.36%、晚班不良品之比率為0.25%。費雪爾正確概率檢定(Fisher’s exact test)的P值為0.6944>0.01,可知兩班輪班工作者生產不良品之比率為無顯著的差異,也就是兩班輪班工作者所生產不良品之比率是相同的。


封面圖-500x383.png)


