本次要探討的主題是在生物統計中常使用的方式-廣義線性模式(GEE),GEE常用於探討多次重複測量的病患研究,詳細的討論說明請往下翻閱~~
一、使用狀況:
廣義估計式(generalized estimating equations, GEE)是由陽明大學校長梁賡義 教授與Scott L. Zeger教授於1986年提出,並於Biometrika及Biometrics陸續發表理論與應用文章,屬於估計方法而非模式方法,用於評估迴歸係數跟標準誤(Standard error)。一般來說,GEE迴歸係數值會跟廣義線性模型(Generalized linear model, GLM) 相近,但標準誤會更為精確,為生物統計學界非常重要的方法,最主要是使用在重複測量(例如:同一個病人去醫院看三次病,每一次的就醫紀錄或生物指標)或鑲嵌(例如:同一個醫生看了很多個病人,考慮醫生之間的差異)的研究上。
二、名詞定義與解釋:
GEE中我們在運算時常使用到共變異數矩陣(covariance structure),用來解釋測量之間的關係,之前我們文章中混合線性模式中也有提到,常見的方式有四種:
非結構化 (Unstructured)、簡易式(Simple)、可交換(Exchangeable)、一階自迴歸模型(First-order autoregressive, AR(1))
1、非結構化 (Unstructured):假設重複測量之間的相關性皆為不同,沒有規律,好用但不易收斂。
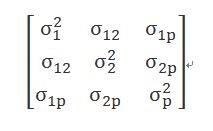
2、簡易式(Simple):測量之間的相關性獨立,不適用於重複測量上
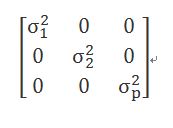
3、可交換(Exchangeable)或稱複合對稱(Compound symmetry):假設重複測量之間的相關性都一樣。Repeated measurement ANOVA的前提假設就是如此。
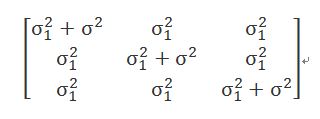
4、一階自迴歸模型(First-order autoregressive, AR(1)):每筆資料和上一個量測有關。
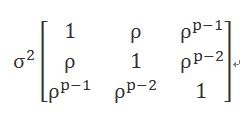
三、前提假設:
GEE使用的前提包含以下幾點
(一)重複量測研究(因為變項之間互相獨立的提假設被打破,故一般常用的統計模式不適合使用)。
(二)屬於半參數方法,不受限於母體分布
(三)應變項可以為連續、順序、類別、計數(count)
(四)個案中有遺漏值仍可以納入分析
四、SPSS 操作Example:
(一)在SPSS中輸入欲分析之資料。
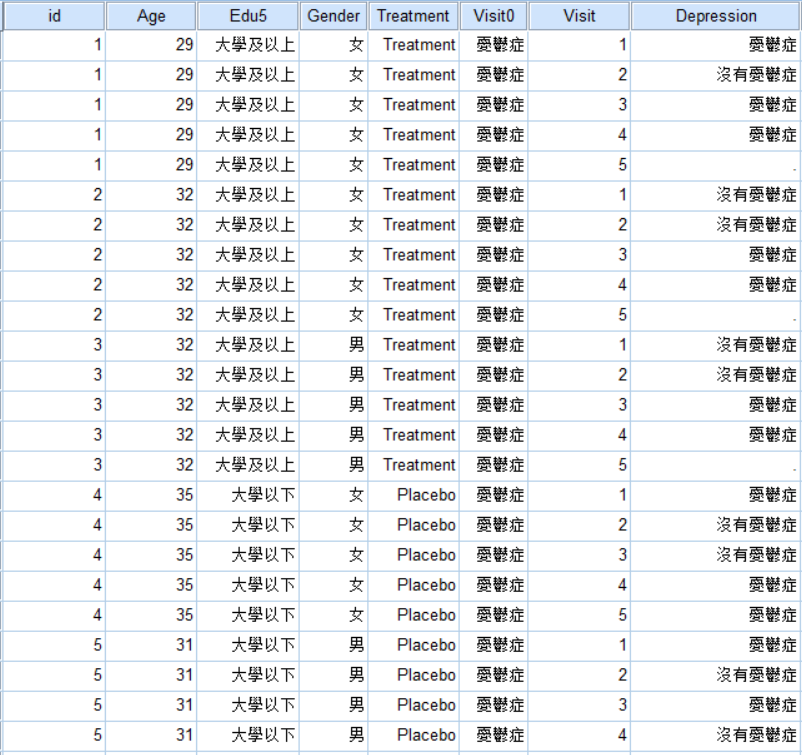
目前有20位憂鬱症病人分別使用藥物治療或安慰劑,我們追蹤了5次就診紀錄,獲得他們每次就醫時的憂鬱狀態,我們利用這筆資料,分析藥物對於憂鬱症的療效。
treatment表示介入的治療方式;Gender表示性別;Visit表示就診時間;Depression表示是否有憂鬱症。
(二)分析→概化線性模式→GEE概化估計方程式
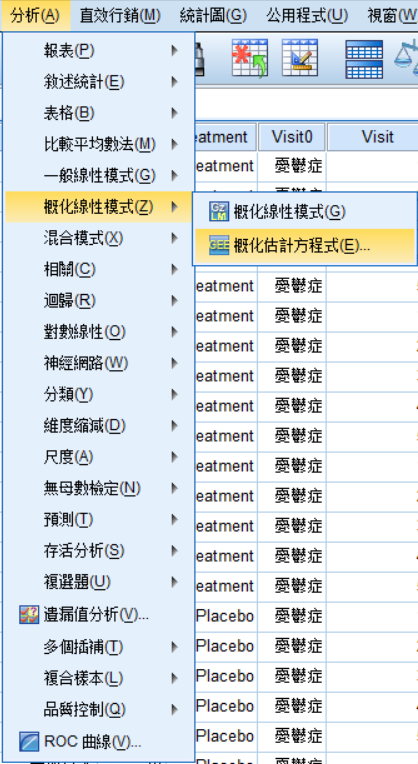
(三)GEE內部操作
1、【重複】
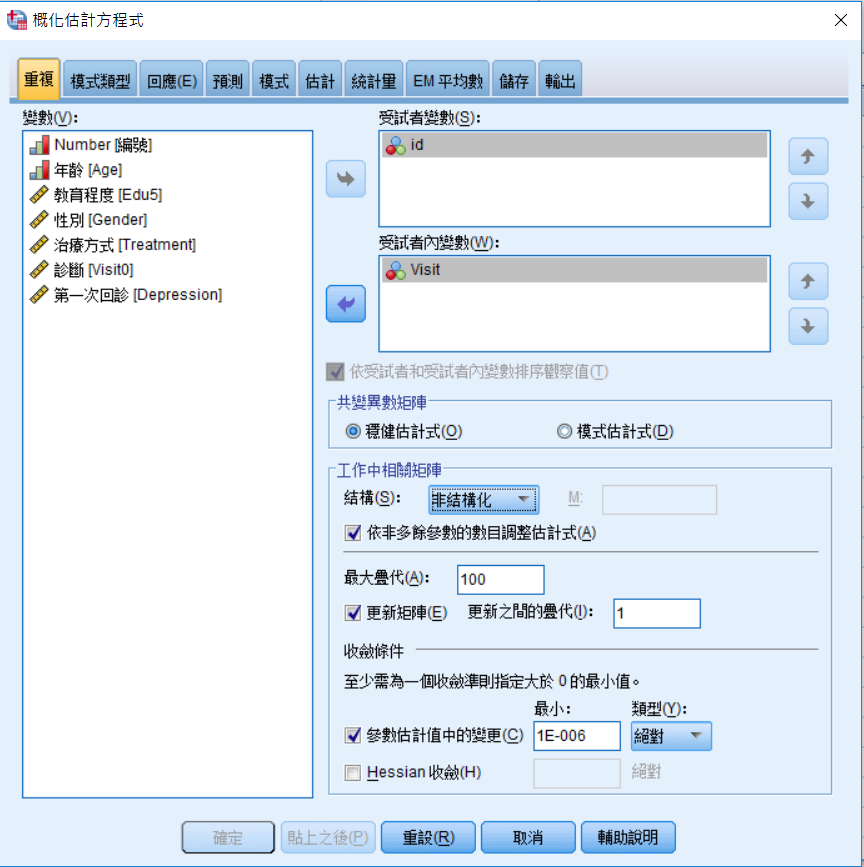
受試者變數:點選ID。
受試者內變數:選Visit
共變數矩陣:如果個案數夠多可以選擇穩健估計式(Robust),如果過少的話可以選擇模式估計式(Model-based estimator)
結構:選非結構化。當你不知道你的資料共變結構的時候,可以先考慮使用非結構化(Unstructured correlation, UN),如果重複量測次數多之後,可以選擇一階自迴歸模型(First-order autoregressive correlation, AR(1))。
2、【模式類型】
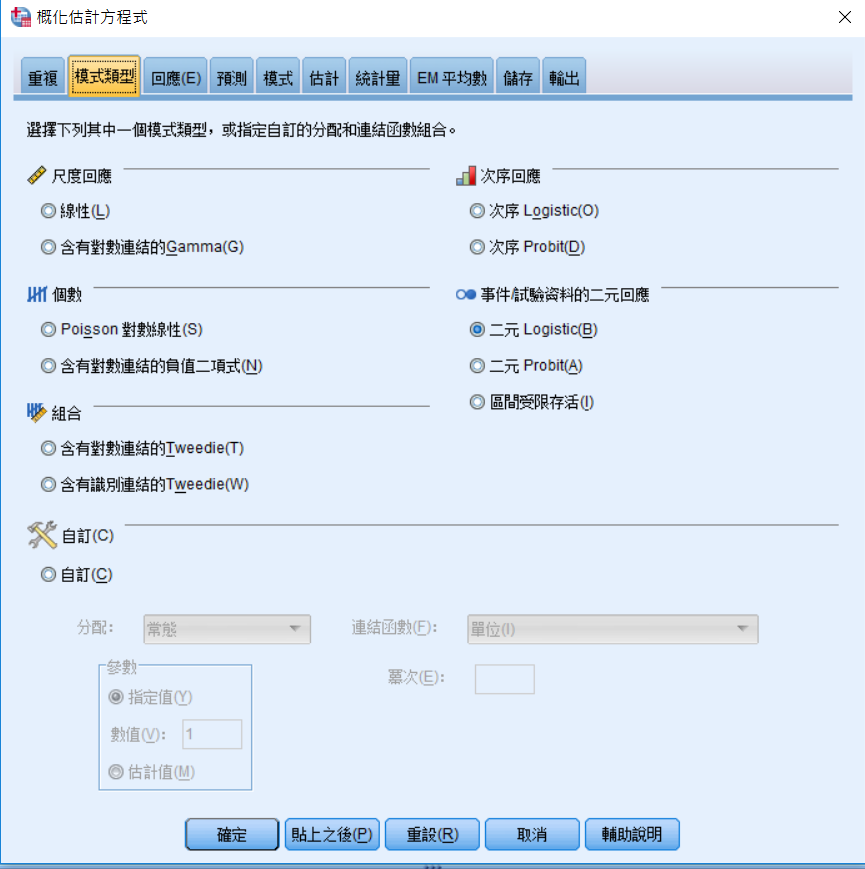
根據應變項是連續、順序、類別、計數來選擇。本次分析資料是以depression為應變項。
3、【回應】
放入應變項depression。
4、【預測】
因子:治療的方式
共變量:教育程度、性別、年齡、回診時間
5、【模式】
這裡的模式也可以放入交互作用,例如年齡跟回診時間的。
6、【估計】跟【統計量】我們就依照原來設定就好。
五、統計結果

透過上表中QIC/QICC可以得知哪個是最好的共變結構假設,數值越小越好。所以研究者可以嘗試跑不同的共變結構假設後,選取QIC/QICC最小的當最後的模型。
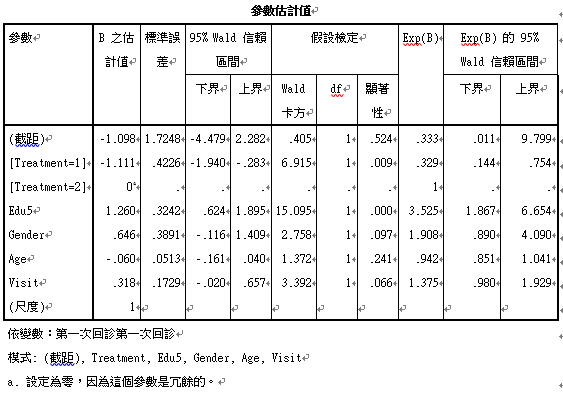
由上表可以看出,控制了性別、教育程度、年齡之後,治療組相較於安慰劑組的OR為0.329,且有達到顯著上的差異(p=0.009),表示治療組得到憂鬱的機率較低,治療是有成效的。但在性別與年齡上未達統計上顯著的差異(p=0.097跟0.241)。


封面圖-500x383.png)


