羅吉斯迴歸主要用於依變數為二維變數(0,1)的時候，以下將詳細說明其原理及SPSS操作。
一、使用狀況
羅吉斯迴歸類似先前介紹過的線性迴歸分析，主要在探討依變數與自變數之間的關係。線性迴歸中的依變數(Y)通常為連續型變數，但羅吉斯迴歸所探討的依變數(Y)主要為類別變數，特別是分成兩類的變數(例如：是或否、有或無、同意或不同意……等）。
＊【小常識】
在羅吉斯迴歸分析中，自變數x可以是類別變數，也可以是連續變數。
二、前提假設
(一) 羅吉斯分配中，自變數對依變數的影響是以指數的方式做變動，因此不需要常態分配的假設。
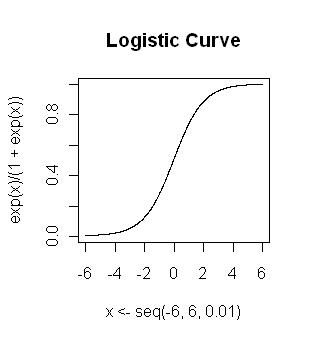
(二)令依變數Y為二元反應的變數(成功或失敗)，p為其成功的機率，受自變數ｘ所影響，則p與ｘ之關係如下：
Y事件成功的機率：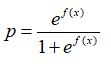
Y事件失敗的機率：
＊【小常識】
p的值介於0~1之間，p接近0時表示Y成功的機會很小，接近1時則表示成功的機會很大
(三) 勝算(Odds)：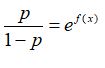 
，即事件成功機率與失敗機率的比值。
以下採實驗設計為例：
| 事件成功 | 事件失敗 | 總和 | |
| 實驗組 | 4
(a) |
16
(b) |
20
(a+b) |
| 對照組 | 1
(c) |
19
(d) |
20
(c+d) |
| 5
(a+c) |
35
(b+d) |
40
(a+b+c+d) |
實驗組的勝算(Experimental event odds) = a/b = 4/16 = 0.25
控制組的勝算(Control event odds) = c/d = 1/19=0.053
勝算比(odds ratio) = (a/b) / (c/d) = ad/bc = 4.72
(四) 羅吉斯迴歸式：對勝算值(Odds)取自然對數(ln)即得之。
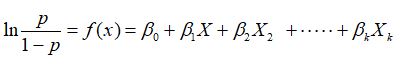
係數值( )→用來計算當 的值增加一單位時勝算的改變量(Δ odds)。
當 Δ odds > 1，表示當Xi 增加時，事件Y 發生的勝算會提高
Δ odds < 1，表示當Xi 增加時，事件Y 發生的勝算會降低
＊【小常識】
Δ odds 又稱為OR值，在SPSS中以EXP(B)表示。
三、假說檢定
羅吉斯迴歸模型的顯著性檢定(F test)：探討羅吉斯迴歸模型中的β係數是否全部為0。當係數不全為0時，迴歸模型才具有預測力。
虛無假說(Null hypothesis)→ 
對立假說(alternative hypothesis)→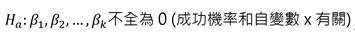 
統計值(Statistics)→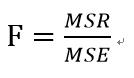
四、SPSS 操作Example
【例題1】某公司欲根據過去「溫度」與「零件測試成功與否」的資料，建立以 溫度預測零件測試成功機率之迴歸模式。
→本題例子為二元羅吉斯迴歸，以一個連續型的自變數(溫度)去預測y(零件測試成功與否)。其中，y=1表示零件測試成功，y=0表示零件測試失敗。
(一)在SPSS中輸入欲分析之資料。
(二)二元羅吉斯迴歸：分析→迴歸→二元Logistic
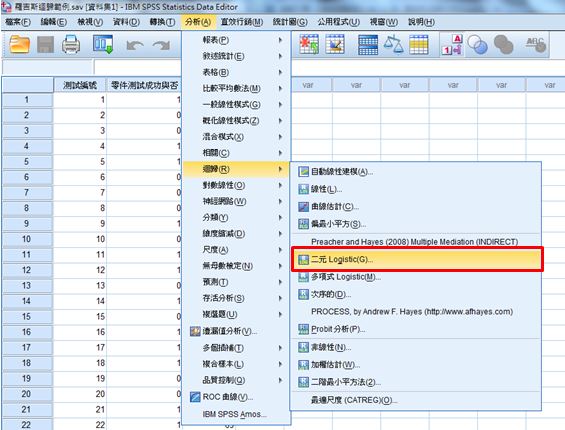
(三) 因變數：零件測試成功與否(y)
共變量：溫度(即自變數x)
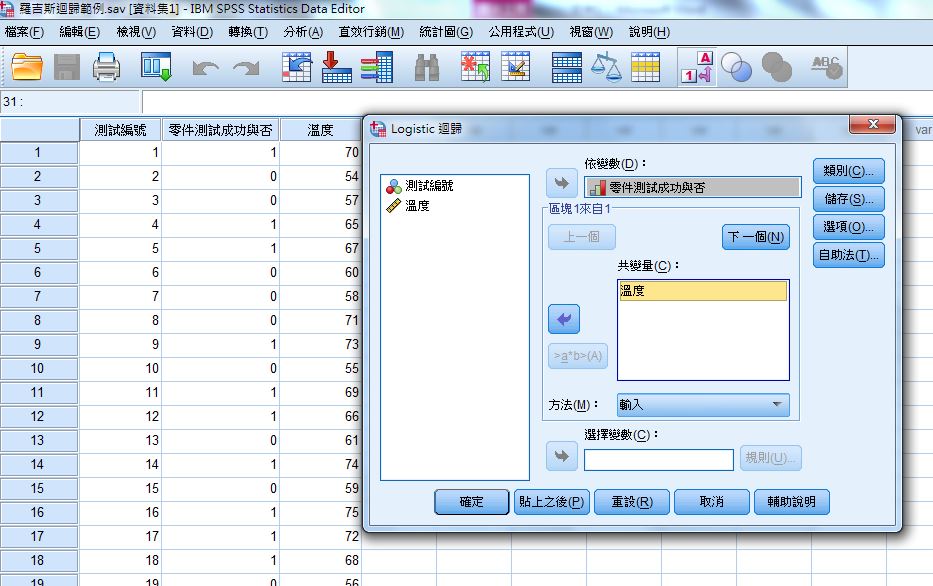
(四) 報表結果：
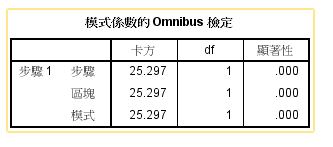
1. 模式係數的Omnibus測試：相當於線性迴歸裡的ANOVA-F檢定，探討羅吉斯迴歸模型中的β係數是否全部為0。
在本例中，顯著性p值<0.001，拒絕虛無假說。
→此羅吉斯迴歸模型顯著，具有預測能力。
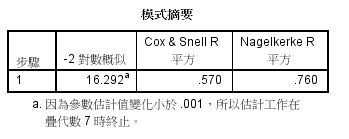
2. 模式摘要：呈現關於解釋力之「-2對數概似」、「Cox-Snell R平方」、
「Nagelkerke R 平方」的值做為參考。
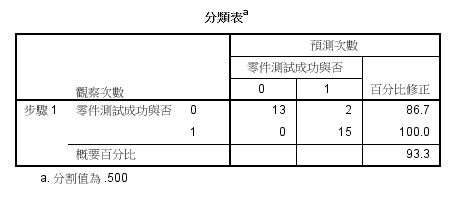
3. 分類表：呈現預測值的準確度。
4.方程式中的變數：可得到羅吉斯迴歸式與Δ odds(OR值)。
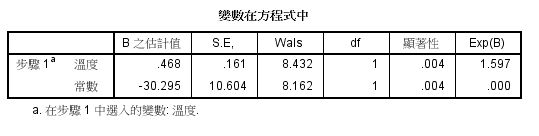
(1) 根據上表我們可以得出以下的羅吉斯迴歸式：
(2) Exp(B)=1.597，即Δ odds=1.597>1，表示溫度每上升一度，零件測試成功機率會比零件測試失敗機率多出1.597倍。
【例題2】某醫療單位欲根據過去肺部疾病就診病患的基本資料，建立以有無「吸菸」、有無「家族病史」預測「罹患肺癌」機率之迴歸模式。
→本題例子為二元羅吉斯迴歸，以兩個類別型的自變數(吸菸、家族病史)去預測y(罹患肺癌與否)。其中，y=1表示罹患肺癌，y=0表示沒有罹患肺癌。
(一)在SPSS中輸入欲分析之資料。
(二)二元羅吉斯迴歸：分析→迴歸→二元Logistic
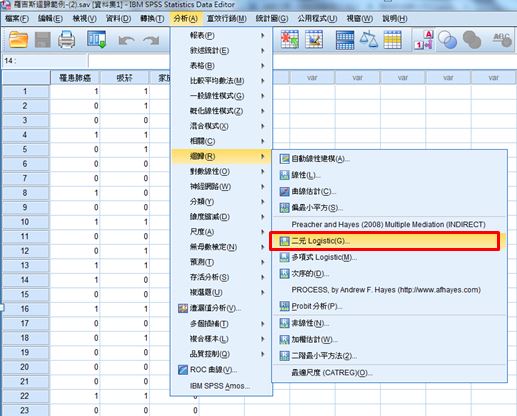
(三) 因變數：罹癌與否(y)
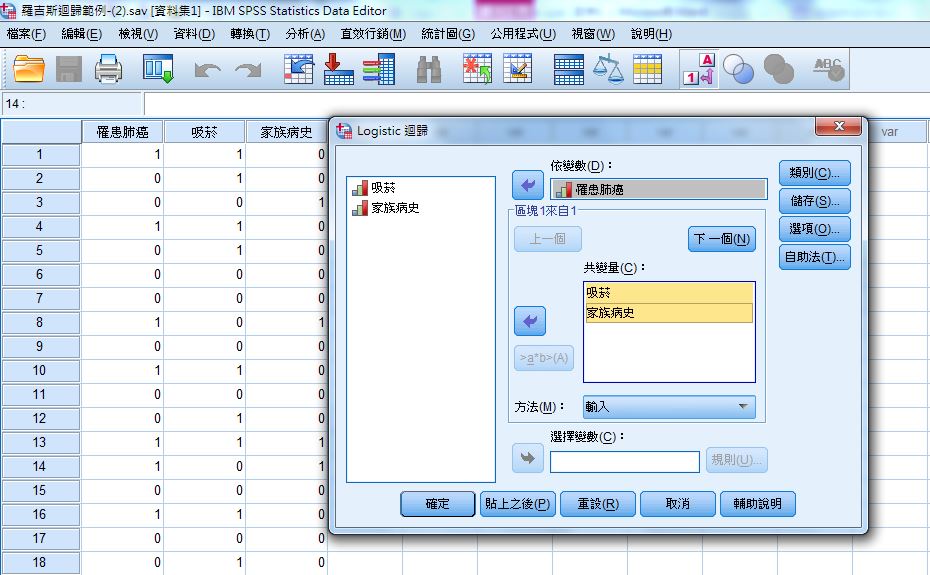
共變量：吸菸與否(即自變數x1)
有無家族病史(即自變數x2)
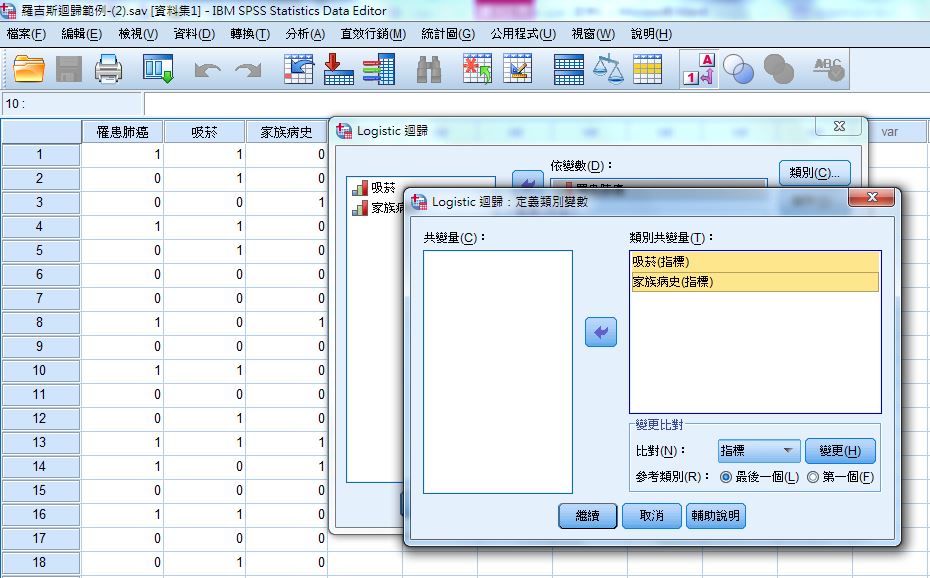
(四)類別→指定類別共變量：吸菸(x1)、家族病史(x2)
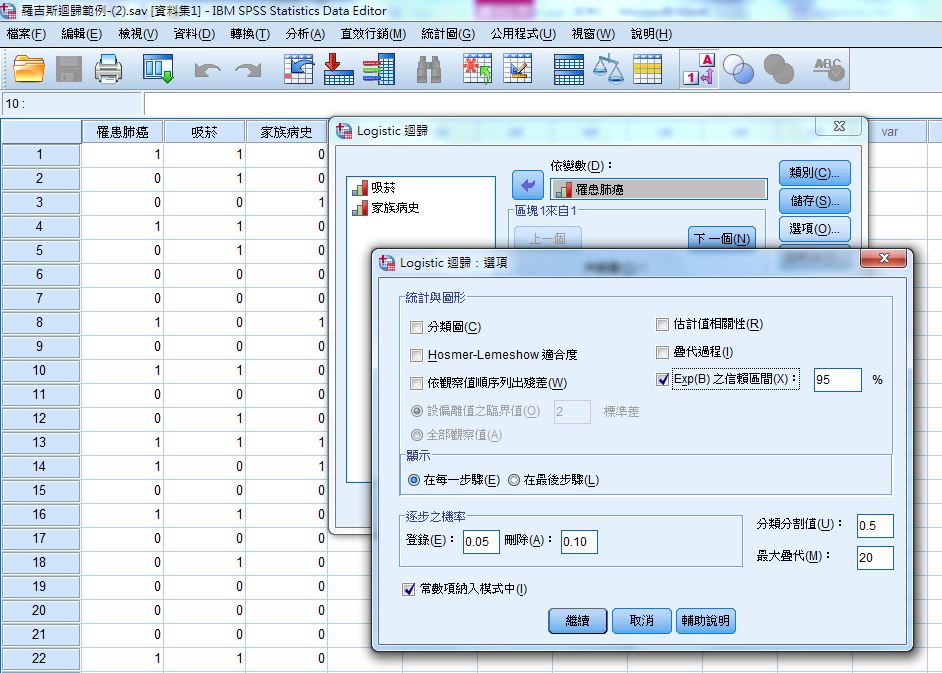
(五) 選項：Exp(B)之信賴區間(X)
(六) 報表結果：
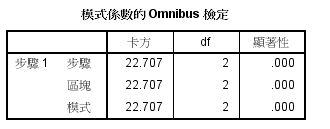
1. 模式係數的Omnibus測試：相當於線性迴歸裡的ANOVA-F檢定，探討羅吉斯迴歸模型中的β係數是否全部為0。
在本例中，顯著性p值<0.001，拒絕虛無假說。
→此羅吉斯迴歸模型顯著，具有預測能力。
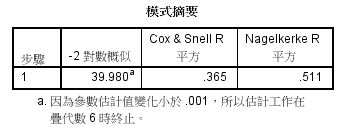
2.模式摘要：呈現關於解釋力之「-2對數概似」、「Cox-Snell R平方」、
「Nagelkerke R 平方」的值做為參考。
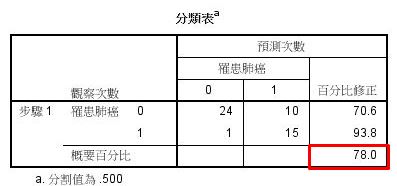
3.分類表：呈現預測值的準確度。
4.方程式中的變數：可得到羅吉斯迴歸式與Δ odds(OR值)。
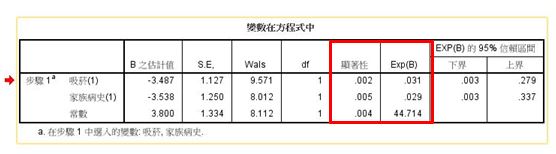
根據上表可知
(1) 吸菸Exp(B)=0.031，即Δ odds=0.031，表示沒有吸菸的人( =0)罹患肺癌的機率是有吸菸的人( =1)罹患肺癌機率的0.031倍。
(2)家族病史Exp(B)=0.029，即Δ odds=0.029，表示沒有家族病史的人( =0)罹患肺癌的機率是有家族病史的人( =1)的0.029倍。
由於上述兩個變數皆達顯著(p<.05)，故我們可以推論此筆病患資料中「罹患肺癌與否」與「吸菸」及「有無家族病史」有直接關係。
本次教學的檔案有兩個範例，檔案如下所示，僅供同學練習使用：
