在許多研究設計中,常會採用變異數分析探討多組群體的平均數是否達顯著差異。
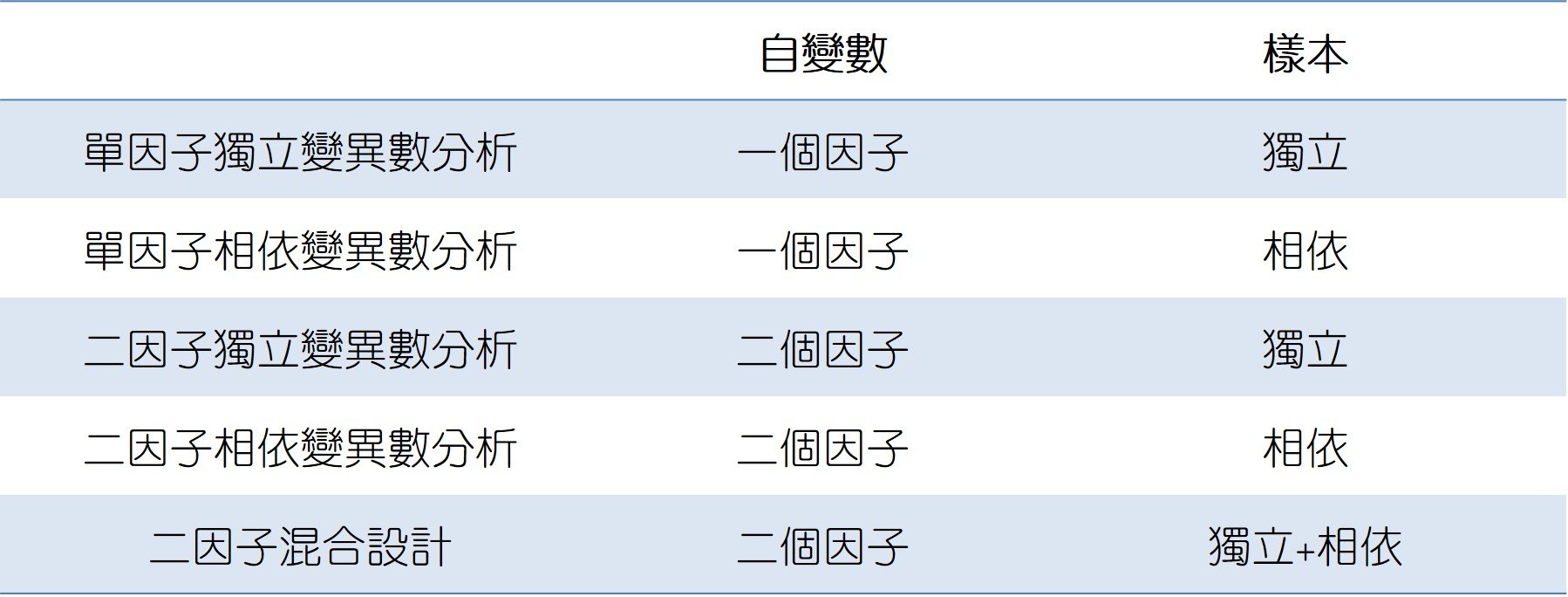
常見的變異數分析可根據自變數為「單因子」或「雙因子」,以及樣本之間的關係屬於「獨立(Independent)」、「相依(Dependent)」抑或「獨立+相依」,分為五種類型的變異數分析,包含:
- 單因子獨立變異數分析(One Way ANOVA, independent samples):單個因子且樣本為獨立。
- 單因子相依變異數分析(One Way ANOVA, paired-sample):單個因子且樣本為相依。
- 二因子獨立變異數分析(Two Way ANOVA, independent samples):雙個因子且樣本為獨立。
- 二因子相依變異數分析(Two Way ANOVA, paired-sample):雙個因子且樣本為相依。
- 二因子混合設計(Two-way ANOVA, mixed design):雙個因子,兩個自變數因子中,一樣本為獨立,另一樣本為相依。
一、使用情況:
過去關於醫護臨床試驗或者是教育心理介入型的研究,多會採取準實驗設計法,實驗組和控制組均於前後測兩個時間點接受調查或檢驗,實驗組會在前後測的時間點中接受實驗或介入處理,此2×2的研究設計,通常會採用二因子混合設計的統計分析方法,驗證介入的成效,其中組間因子為實驗組和控制組(獨立樣本),組內因子為前測和後測(相依樣本)。
二、前提假設:
1、依變數(Dependent variable):
(1)、必須是連續變數(continuous variable)
(2)、必須為隨機樣本(Random variable)→從母群體(Population)中隨機抽樣得 到
(3)、母群體:必須是常態分佈(Normal Distribution)
2、相依事件(Dependent event):樣本須為相依(Dependent)
3、變異數(Variance):兩組樣本的變異數必須相等(同質)。
三、假說檢定(Hypothesis Testing):
1、兩因子間是否有交互作用?
交互作用表示不同因子在依變數上的差異達顯著,說明兩因子間會相互影響。
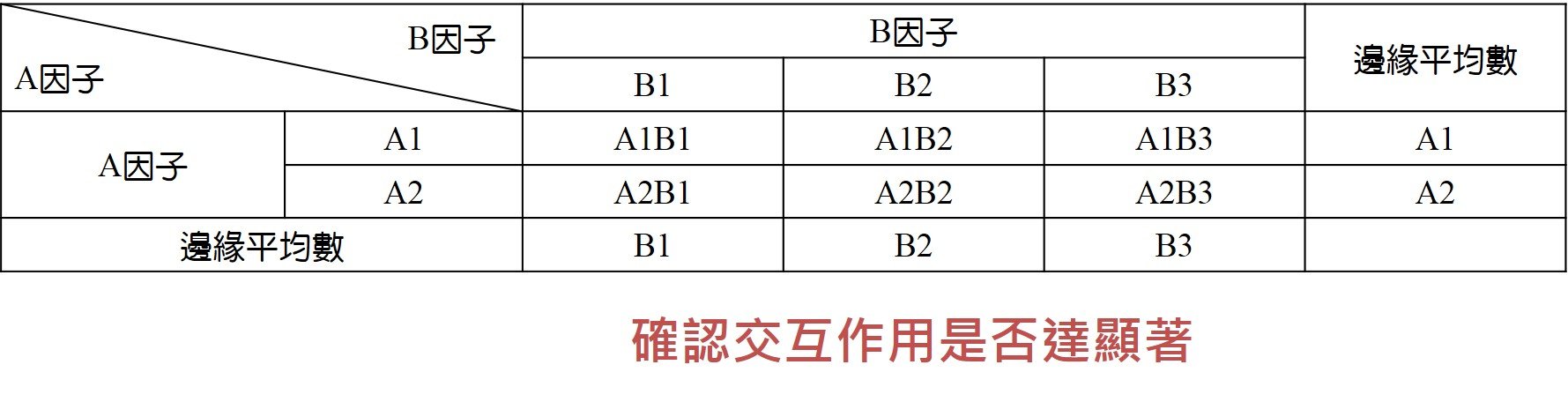
2、A因子處理間平均數是否相等?
虛無假說(Null hypothesis)→????0:u1 = u2 = u3=…= uk
對立假說(alternative hypothesis)→????????:至少一組u不相等
統計值(Statistics)→ F = MSB/MSW ,F值愈大→組間(相對於組內)差異愈大
3、B因子處理間平均數是否相等?
虛無假說(Null hypothesis)→????0:u1 = u2 = u3=…= uk
對立假說(alternative hypothesis)→????????:至少一組u不相等
統計值(Statistics)→ F = MSB/MSW ,F值愈大→組間(相對於組內)差異愈大
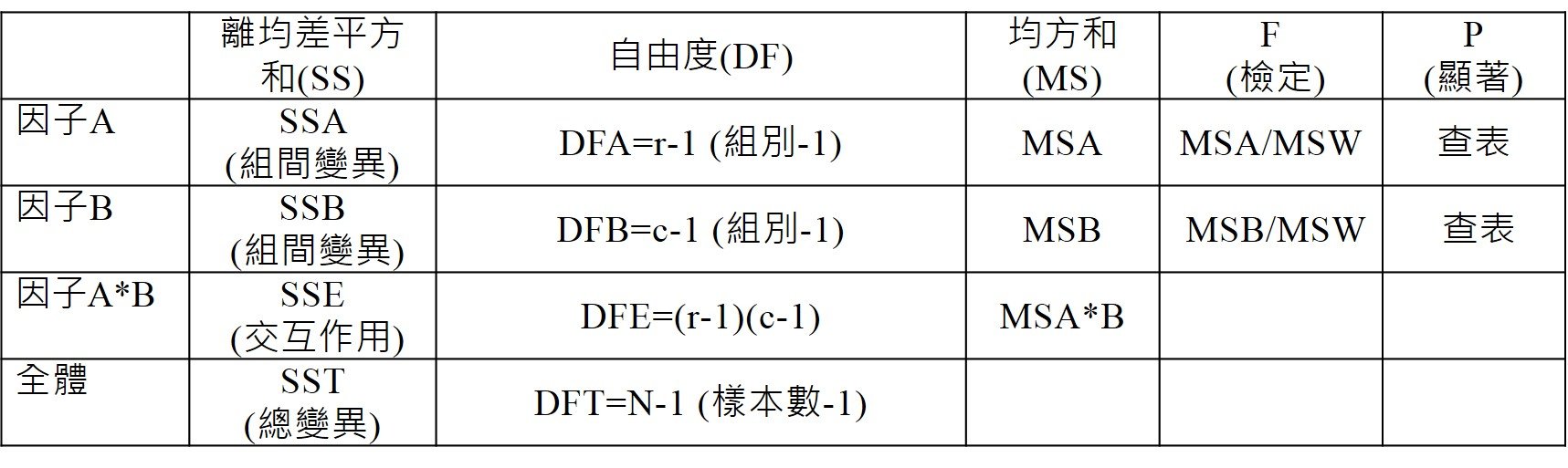
四、分析步驟
1、確認A×B因子是否達顯著的交互作用。
2、若A×B因子的交互作用未達顯著時,進行主要效果(Simple)比較
(1)、比較A因子的邊緣平均數,查看其中A1與A2哪個組別得分較高。
(2)、比較B因子的邊緣平均數,即比較B1、B2與B3哪個組別得分較高。
3、若A×B因子的交互作用達顯著時,進行單純主要效果(Simple main effect):
(1)、A因子的單純主要效果檢定:
當限定於B因子=b1水準時,H0:μa1b1=μa2b1
當限定於B因子=b2水準時,H0:μa1b2=μa2b2
當限定於B因子=b3水準時,H0:μa1b3=μa2b3
(2)、B因子的單純主要效果檢定:
當限定於A因子=a1水準時,H0:μa1b1=μa1b2=μa1b3
當限定於A因子=a2水準時,H0:μa2b1=μa2b2=μa2b3
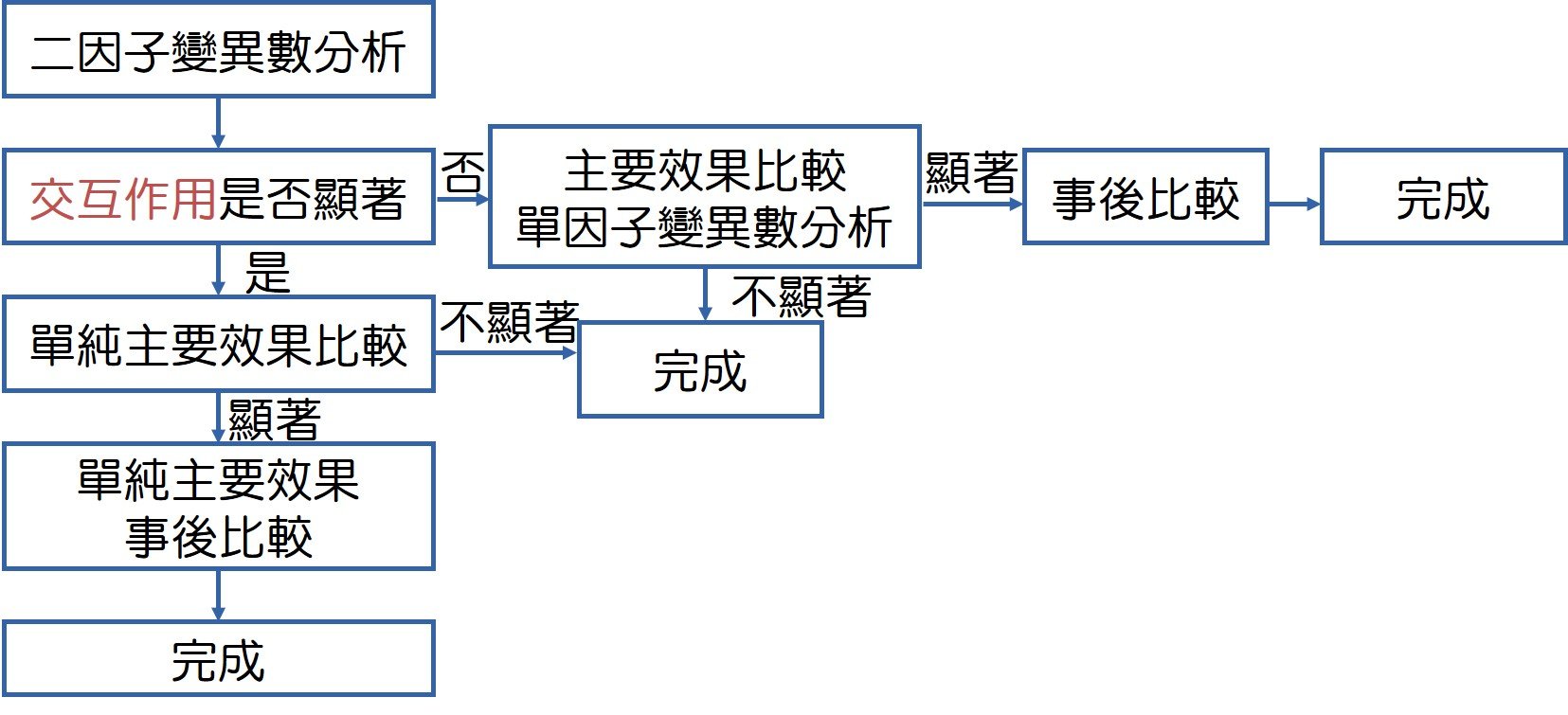
當A×B因子的交互作用達顯著時,試驗和介入的確具有實質上的成效。
詳細的資訊內容建議查看永析官網的統計實務介紹(http://www.yongxi-stat.com/),以及其他統計分析相關的專書。
參考資料
吳明隆與涂金堂(2014)。SPSS 與統計應用分析。台北:五南。
邱皓政(2002)。量化研究與統計分析:SPSS中文視窗版資料分析範例解析。台北:五南。


封面圖-500x383.png)


