為實驗組中發生結果的勝算(Odds)與對照組中發生結果的勝算,此兩者間的比值就稱為勝算比(OR)。
本篇文章主要介紹勝算比 – R語言的操作,細節如下所述。
一、勝算比的計算方式
通常被使用於個案對照研究之中。
為實驗組中發生結果的勝算(Odds)與對照組中發生結果的勝算,此兩者間的比值就稱為勝算比(OR)。
各組的勝算為研究過程中各組發生某一事件之人數除以沒有發生某一事件之人數。
當發生此一事件之可能性極低時,則相對危險比(RR)幾近於勝算比(OR)。
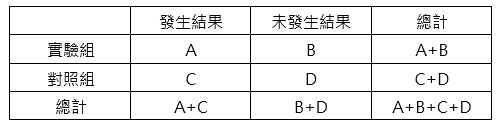
以附表為例:實驗組中發生結果的勝算= A/B,對照組中發生結果的勝算= C/D,勝算比= (A/B) / (C/D) = AD/BC。
二、R語言操作範例
(一) 範例介紹
某研究員想研究糖尿病(Diabetes)的危險因素,在某地區抽樣調查了385名35歲以上居民得到糖尿病的情況得如下表:
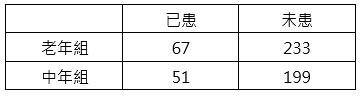
試以顯著水準α = 0.01,檢定居民的年齡與患糖尿病的風險彼此是否獨立及計算老年人得到糖尿病的風險是中年人的幾倍?
(1) 假設檢定
虛無假設→ H0:居民的年齡與患糖尿病的風險彼此間獨立。
對立假設→ H1:居民的年齡與患糖尿病的風險彼此間不為獨立。
(2) 顯著水準 α = 0.01
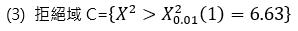
(二) 資料匯入
Diabetes<-read.csv(“Diabetes-7.csv”,header=T)
# read.csv ():將資料匯入到指定的變數,也就是Diabetes
View(Diabetes)
# View():瀏覽資料內容
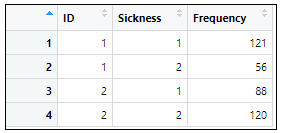
=>根據執行結果:在資料集中共有3個變數和4個觀察資料,3個變數分別為:
分類(ID):1.老年組(≥60歲)、2.中年組(35-59歲);患病程度(Sickness):1.已患糖尿病者、2.未患糖尿病者;頻率(Frequency)
(三) 統計描述及推斷
- 資料整理
data<-data.matrix(Diabetes$Frequency) #取Frequency資料轉矩陣格式
rname<-c(“elderly”,”midlife”) #行名稱
cname<-c(“Yes”,”No”) #列名稱
compare<-matrix(data,nrow=2,ncol=2,dimnames=list(rname,cname)) #資料整理並編輯為矩陣格式
compare #查看數據
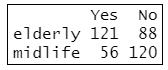
=>根據執行結果:列出了卡方檢定所需要的資料格式,並存儲在「compare」資料框中
- 計算構成比
S1<-prop.table(compare, margin = 2) #計算列百分比
S1 #顯示列百分比

=>根據執行結果:列出已患糖尿病者和未患糖尿病者兩組人群中老年組和中年組的百分比。可知已患糖尿病的老年組占68.4%、未患糖尿病的老年組占42.3%
- 卡方檢定
S2<-chisq.test(compare,correct = FALSE) #不進行連續性校正
S2$expected #查看期望次數

=>根據執行結果:可知表格內的期望次數均>5,最小期望值為80.91429。
# 補充:在卡方檢定中,一般要求期望次數不得小於1,並且不得有20%以上細格的期望次數小於5。
不然則建議合併相鄰的行或列,或採用連續性校正Yate’ s correct test,亦或採用Fisher’ s Exact Test。
S2 #查看卡方檢定結果

=>根據執行結果:顯示卡方統計量、自由度和P值。可知居民的年齡與患糖尿病的風險是有顯著的差異(χ2=26.157,P<0.01)。
#補充:當自由度等於1是否需要進行校正?
在理論上,當自由度等於1時,一定要進行連續校正。
但在實務上,當所有細格內的期望次數≥10時,並不須進行校正,因為校不校正對檢定效率的影響很小,亦即校正前後的卡方值很接近。
- 計算OR值
install.packages(“epiDisplay”) #安裝套件:epiDisplay
library(epiDisplay) #載入套件:epiDisplay
cci(cctable=compare) #計算OR值
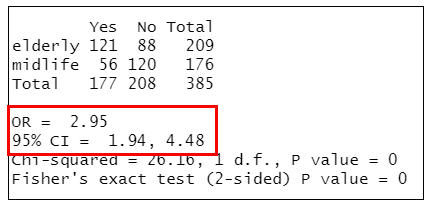
=>根據執行結果:可知老年組得到糖尿病的風險是中年組的2.95倍[OR=(121×120)/(88×56)],OR值的95% CI為1.94~4.48。
三、結論
本研究採用卡方獨立性檢定對居民的年齡與患糖尿病的風險彼此間是否獨立進行比較和計算比值比。
結果顯示,已患糖尿病的人群中老年組占68.4%、未患糖尿病的人群中老年組占42.3%,居民的年齡與患糖尿病的風險是有顯著的差異(χ2=26.157,P<0.01),表明居民的年齡與患糖尿病的風險彼此間不為獨立,也就是拒絕H0接受H1。
另外老年人得到糖尿病的風險是中年人的2.95(95%CI: 1.94-4.48 )倍,即高齡是患糖尿病的危險因素。


封面圖-500x383.png)


