單因子變異數分析(ANOVA)用於比較多組之間的平均數差異,若組別效果顯著的話,則會進行事後比較確認各組的差異情形,詳細說明如下。
一、使用狀況:
比較多組(兩組以上)樣本平均數是否相等。
變異數分析是用來檢定多組樣本平均數是否相等,並非在檢定變異數。
單因子變異數分析(One-way ANOVA):只有一個自變項的變異數分析。
獨立樣本(Independent Sample):比較青年、中年、老年三個年齡層的族群,對於飲料甜度的喜好是否不同。
因此獨立樣本單因子變異數分析適用於檢定多組獨立樣本間是否有平均數差異。
二、前提假設:
1.自變數為類別變數(categorical variable),依變數必須是連續變數(continuous variable)
2. 母群體必須是常態分佈(Normal Distribution)
3. 獨立事件(Independent event):樣本須為獨立變項(Independent variable)→第一組的樣本不影響第二組的樣本;第二組的樣本也不影響第一組。
例如:分析從日本、美國兩地進口的蘋果與台灣當地的蘋果甜度是否有差異,從日本或美國進口與台灣當地的蘋果這三組樣本量測不會互相影響
4. 變異數(Variance)同質性:兩組樣本的變異數必須相等。
*【小常識】
單因子變異數分析還有其他幾種不同的變形
重複量測變異數分析→當樣本不是獨立事件時
多因子變異數分析→當樣本有多個自變項時
三、假說檢定(Hypothesis Testing):
| 離均差平方和(SS) | 自由度(DF) | 均方和(MS) | F (檢定) | P (顯著) | |
| 組間 | SSB (組間變異) | DFB=K-1 (組別-1) | MSB | MSB/MSW | 查表 |
| 組內 | SSW (組內變異) | DFW=(N-1)-(K-1)=N-K | MSW | ||
| 全體 | SST (總變異) | DFT=N-1 (樣本數-1) |
數學公式:SST=SSB+ SSw
總變異(Total Sum of Square Error, SST):SST
組間變異量(Between Group Sum of Square Error, SSB):SSB
組間均方和(Between Group Mean of Square Error, MSB):MSB=SSB/DFB
組內均方和(Within Group Mean of Square Error, MSw):MSW=SSW/DFW
One-way ANOVA:比較組間(相對於組內)是否有顯著差異
虛無假說(Null hypothesis)→H0: 各組平均數皆相等
對立假說(alternative hypothesis)→H1: 至少有兩組之間的平均數不相等
統計值(Statistics)→F值愈大→組間(相對於組內)差異愈大
四、SPSS 操作範例:
【例題】比較青年、中年、老年三個年齡層的族群,對於飲料甜度的喜好是否不同?
本題的例子為三組比較,故選擇One-Way ANOVA檢測三組樣本的平均值是否不同
(一)在SPSS中輸入欲分析之資料。
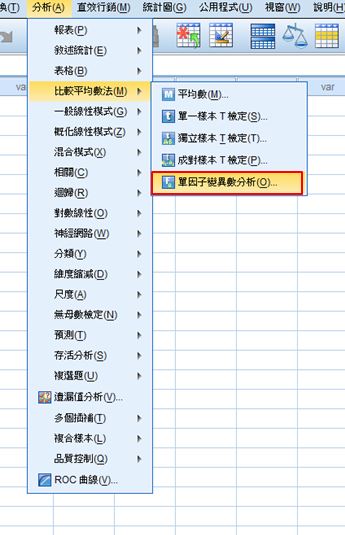
(二)One-Way ANOVA:分析→比較平均數法→單因子變異數分析
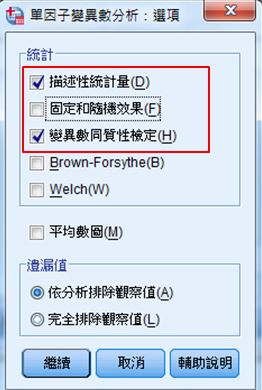
選擇描述性統計量及變異數同質性檢定。
(三)依變數:習慣飲料甜度(SweetDrink),因子:年齡(AgeRange)
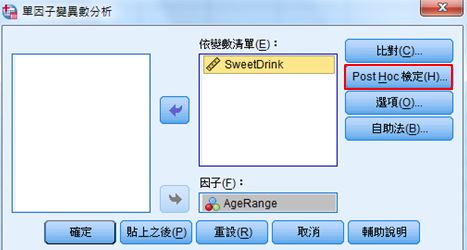
Post Hoc檢定:可選擇欲呈現的事後檢定的方式
一般Scheffe’比較嚴格,LSD比較不嚴格,本研究採用Bonferroni & Tukey,
屬於適中的嚴格程度。
(四)檢定結果:
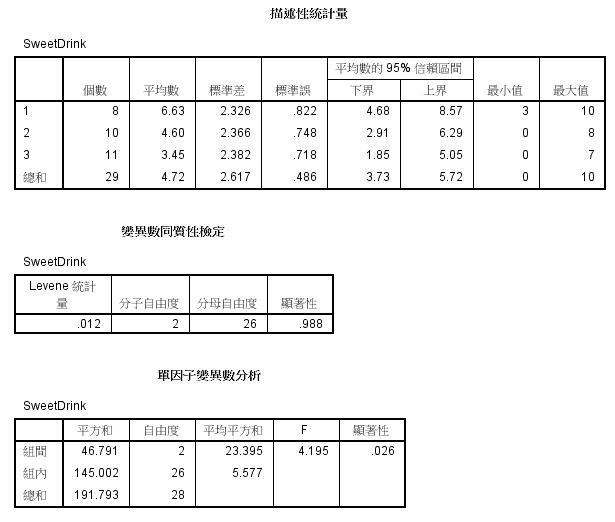
1.基本描述性統計:
分別有8位青年、10位成年及11為老年人包含在本次分析中。
青年的習慣甜度平均為6.63,標準差為2.326
成年的習慣甜度平均為4.60,標準差為2.366
老年的習慣甜度平均為3.45,標準差為2.328
全體的習慣甜度平均為4.72,標準差為2.617
2.變異數同質檢定 (Levene檢定):
在本例中,F檢定後的結果,顯著性p值=0.988>0.05,三組變異數並無顯著差異(同質)。
3.單因子變異數分析:
在本例中,計算後的F統計值為4.195,顯著性p值=0.026<0.05,拒絕虛無假說。
→青年、中年、老年三個年齡層的族群,對於飲料甜度的喜好有顯著不同。
事後檢定(Post hoc):為檢定當多組樣本平均數有顯著差異時,詳細的顯著差異是發生在哪幾組之間。
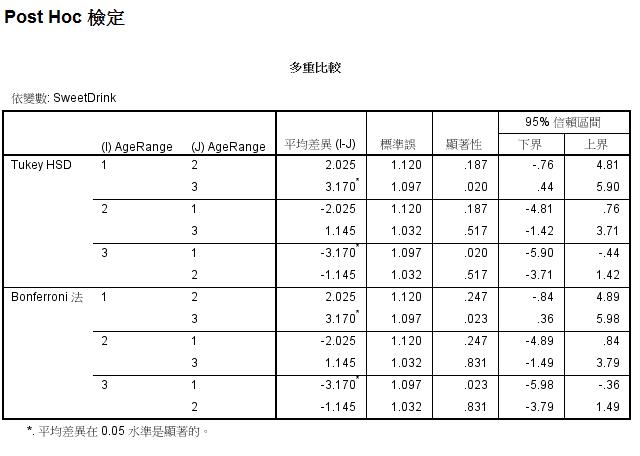
關於事後檢定有許多種檢定方式,本次以Tukey及Bonferroni法為例,兩種方法的結果皆顯示顯著性差異發生在青年與老年兩組之間。
本文SPSS操作範例可從以下連結下載,僅供同學練習使用:
五、R code操作範例 :
## Default
aov(response ~ factor, data=data_name)
TukeyHSD(result,conf.level=0.95)
【例題】分析從日本、美國兩地進口的蘋果與台灣當地的蘋果甜度是否有差異?
本題的例子為三組獨立樣本比較,故選擇One Way ANOVA檢測兩組樣本的平均值是否不同
→輸入日本進口(Japan)、美國進口(America)與台灣本地(Taiwan)的蘋果甜度
Sweet=c(3,5,8,6,4,9,2,7,1,5,10,6,7,8,3,1,6,9,9,8,7,3,2,8)
Region=c(rep("Japan",8),rep("America",8),rep("Taiwan",8))
SweetTest=data.frame(Sweet,Region)
繪圖:plot(Sweet~Region,data=SweetTest)
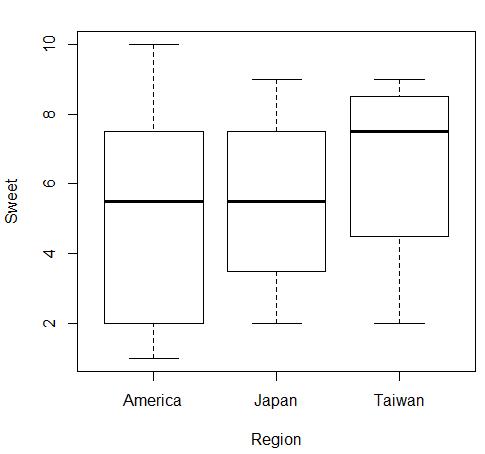
進行ANOVA檢定:
result=aov(Sweet~Region,data=SweetTest)
summary(result)
Df Sum Sq Mean Sq F value Pr(>F)
Region 2 8.08 4.042 0.509 0.609
Residuals 21 166.88 7.946
→結果顯示F檢定值=0.509,顯著性p值=0.609>0.05,三地區的蘋果沒有顯著差異。
接著進行事後檢定:
→事後檢定(Post hoc):用Tukey法檢定兩兩之間是否有顯著性差異(本例原已無顯著差異,本應不用做此步驟)
TukeyHSD(result,conf.level=0.95)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = Sweet ~ Region, data = SweetTest)
$Region
diff lwr upr p-value
Japan-America 0.375 -3.177669 3.927669 0.9618008
Taiwan-America 1.375 -2.177669 4.927669 0.5999142
Taiwan-Japan 1.000 -2.552669 4.552669 0.7606256
→結果p value皆大於0.05,顯示兩兩間皆沒有顯著差異。


封面圖-500x383.png)


