主要用於分析排除第三變項影響後,兩變數之間的關聯性。
以下將用一個範例來輔助說明如何使用R語言來操作。
#補充:淨相關的相關說明可參考:
https://www.yongxi-stat.com/partial-correlation/
一、適用條件
使用Pearson偏相關性分析,需要滿足4個條件:
條件1. 變數類型為連續變數,例如:身高、體重、胸圍。
條件2. 兩變數之間為線性關係,可以用散佈圖來檢驗。
條件3. 兩變數沒有明顯的離群值,可以用箱型圖來檢驗。
#補充:Outlier(異常值或離群值):超過最小值(Q3+1.5 IQR)或最大值(Q1-1.5 IQR)的數值。
條件4. 兩變數要是常態分配或輕微的偏態,可以用分位圖或進行常態性檢驗。
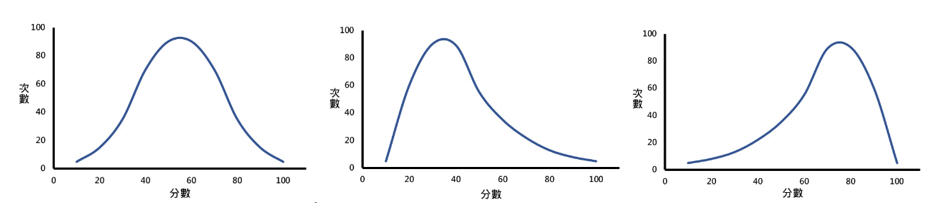
圖1. 常態分配、偏態分配(正偏態、負偏態)
二、R語言操作範例
(一) 範例介紹
探討英文成績與使用次數之關係,控制變項為智力。
研究假設如下:
虛無假設H0:控制智力的影響後,英文成績與使用次數之關係為無相關。
對立假設H1:控制智力的影響後,英文成績與使用次數之關係為有相關。
(二) 資料匯入
CopcData<-read.csv(“Copc.csv”,header=T) # 將資料匯入到指定的變數,也就是CopcData
View(CopcData) #瀏覽資料內容
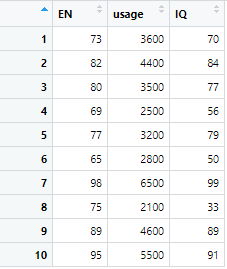
圖2. 資料中EN為英文成績、usage為使用次數、IQ為智力。
(三) 適用條件判定
本範例的英文成績與使用次數之關係,兩變數都是連續變數,滿足適用條件1「變數類型為連續變數」。
1. 線性關係檢測
這裡的檢測方式採用散佈圖,用來判別資料之間,是否有線性相關聯性
#補充:散佈圖(Scatter Plot)
是表示兩個變數之間關係的圖,又稱相關圖。
依下列(A)~(F)的判斷方式,檢視是否為不相關。
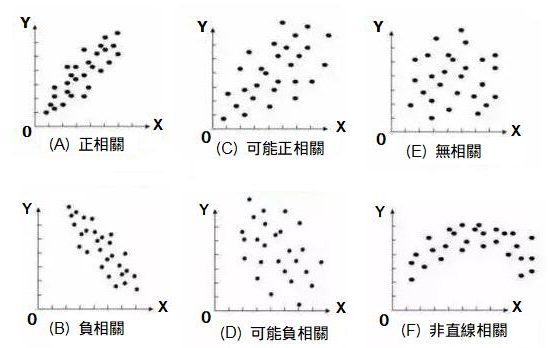
圖3. 散佈圖的判斷方式
##線性關係判斷##
install.packages(“ggplot2”) #安裝套件:ggplot2
library(ggplot2) #載入套件:ggplot2
ggplot(data=CopcData,aes(x=EN,y=usage))+geom_point()+stat_smooth(method=”lm”,se=TRUE) #繪製散佈圖
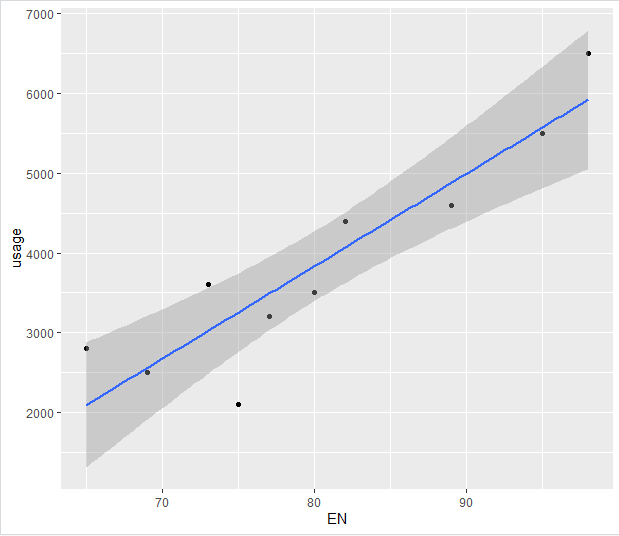
圖4. 英文成績(EN)和使用次數(usage)的散佈圖
=> 據執行結果:英文成績與使用次數呈線性相關(正相關),滿足適用條件2「兩變數之間為線性關係」。
2.離群值檢測
這裡的檢測方式採用箱型圖,來判別資料內是否存在離群值。
#補充:箱型圖(Box plot)
主要是用來顯示數據分佈情況。其組成要素為最小值、第一四分位數、中位數、第三四分位數以及最大值。
箱型圖能夠顯示出離群值(outlier),離群值也叫做異常值,通過箱型圖能夠很容易識別出資料中的異常值。
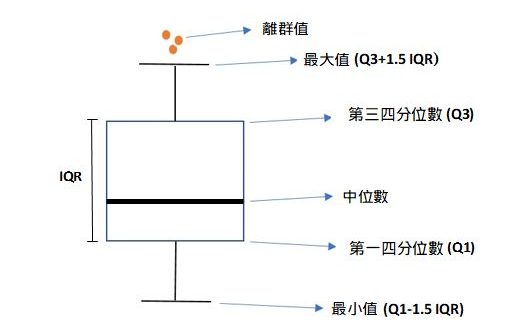
圖5. 箱型圖
(1) ##繪製箱型圖##
par(mfrow=c(1,2)) #繪製一行2個圖
boxplot(CopcData$EN,xlab = c(“EN”), ylab = expression(“score”)) #繪製英文成績的箱型圖
boxplot(CopcData$usage,xlab = c(“usage”), ylab = expression(“frequency”)) #繪製usage的箱型圖
par(mfrow = c(1, 1)) #設置1行1個圖(預設)
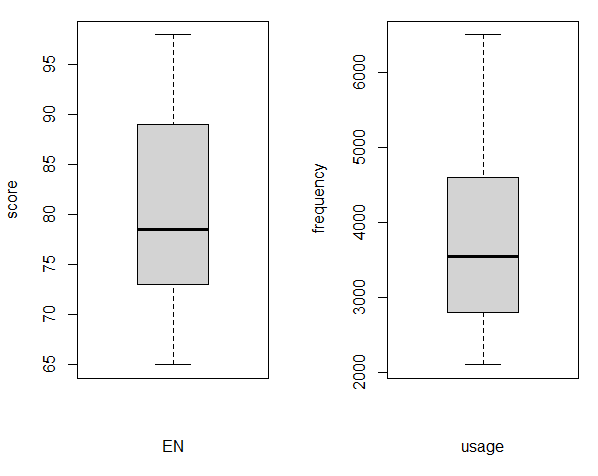
圖6. 分別為英文成績(左圖:EN)和使用次數(右圖:usage)的箱型圖
=>根據執行結果:英文成績和使用次數無明顯異常值。
(2) ##檢查資料最大最小值##
summary(CopcData$EN) #描述EN變數

summary(CopcData$usage) #描述usage變數

=> 根據執行結果:列出了兩變數的最小值和最大值。
依據判斷英文成績可能存在65和98,使用次數可能存在2100和6500的情況。
結合(1)(2)的結果,未發現需要處理的異常值,滿足適用條件3「兩變數沒有明顯的異常值」。
3. 常態性檢測
這裡的檢測方式採用分位元圖(Q-Q圖)和Shapiro-Wilk檢定來做是否為常態分配。
#補充:分位圖(Q-Q圖)
是一種視覺化比較兩項數據的分佈是否相同的方法。
另外,Q-Q Plot不是只有判斷「是否為直線」或者「是否為常態分配」,即使畫出來的不是直線,還是能看出資料分配的特性。
從圖7中可以看到Q-Q Plot在左偏與右偏分配會呈現的樣子:
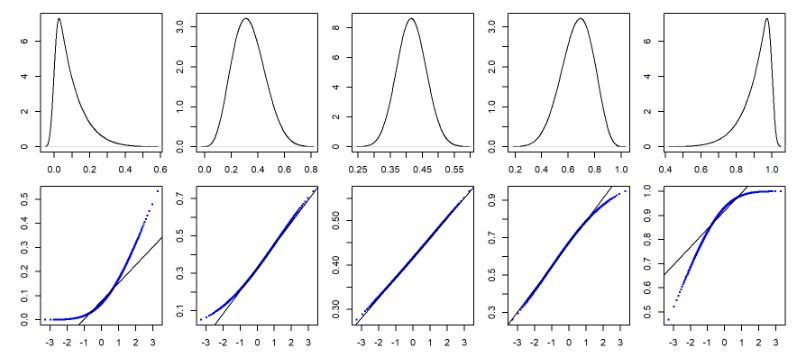
圖7. 不同數值分配下的不同 Q-Q Plot(Source: Manny Gimond https://mgimond.github.io/ES218/Week06a.html)
(1) ##繪製QQ圖##
par(mfrow = c(1, 2)) #設置1行2個圖
qqnorm(CopcData$EN, ylab=”score”, main=”EN”) #繪製英文成績的qq圖
qqline(CopcData$EN) #增加趨勢線
qqnorm(CopcData$usage, ylab=”frequency”, main=”usage”) #繪製使用次數的qq圖
qqline(CopcData$usage) #增加趨勢線
par(mfrow = c(1, 1)) #設置1行1個圖(預設)
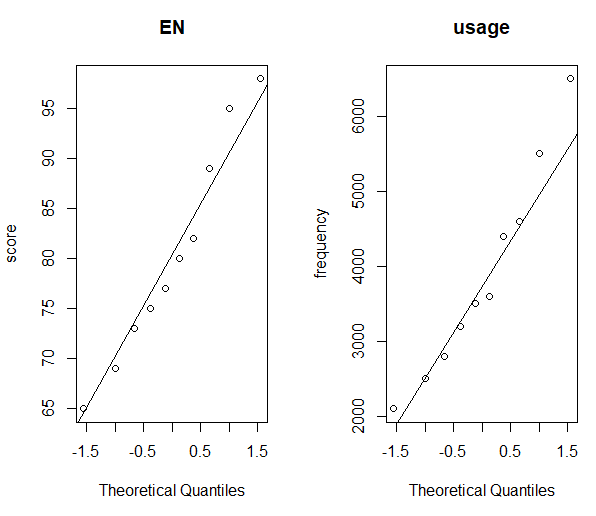
圖8. 分別為英文成績(左)與使用次數(右)的Q-Q圖
=> 根據執行結果:英文成績和使用次數呈常態分配。
#補充:使用Shapiro-Wilk檢定的原因
要進行常態性檢定有兩種方法K-S檢定或S-W檢定,因樣本數的關係而選擇使用S-W檢定。
Kolmogorov-Smirnov(K-S)檢定:樣本數50個以上。
Shapiro-Wilk(S-W)檢定:樣本數50個以下。
(2) ##常態性檢驗##
shapiro.test(CopcData$EN) #檢驗英文成績的常態性
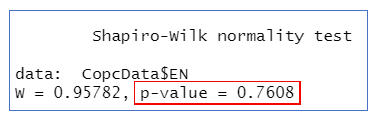
shapiro.test(CopcData$usage) #檢驗使用次數的常態性
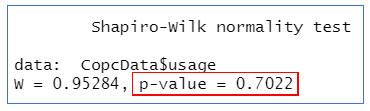
=>根據執行結果:兩變數的常態性檢驗的P值均>0.1,滿足常態性要求。
結合(1)(2)的結果,表示兩變數的資料滿足適用條件4「兩變數為常態分配」。
(四) 統計描述及推斷
(1) ##描述統計##
install.packages(“psych “) #安裝套件:psych
library(psych) #載入套件:psych
describe(CopcData$EN) # EN變數描述統計

describe(CopcData$usage) # usage變數描述統計

describe(CopcData$IQ) # IQ變數描述統計

(2) ##偏相關分析##
install.packages(“ggm”) #安裝套件:ggm
library(ggm) #載入套件:ggm
s<-cov(CopcData) #計算共變異數 (covariance, 又稱協方差)
r<-pcor(c(2,3,1),s) #計算偏相關係數
n<-dim(CopcData)[1] #計算樣本數
pcor_test<-pcor.test(r,1,n) #偏相關係數顯著性檢驗
cor_test<-cor.test(CopcData$EN, CopcData$usage) #計算相關係數顯著性
r #顯示偏相關係數

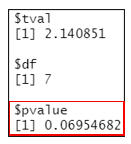
pcor_test #顯示偏相關係數P值
cor_test #顯示相關係數及其P值
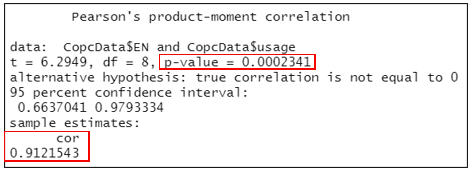
=>根據執行結果:可知英文成績為80.3±10.86分、使用次數為3870±1382.47次、智力為72.8±20.7。
結合(1)(2)的結果可知:
當不控制智力(IQ)時,”EN”和”usage”之間的相關係數r =0.912,P<0.001。即英文成績和使用次數為強相關,且有顯著性。
當控制智力(IQ)時,”EN”和”usage”之間的偏相關係數r =0.629,P>0.05。即英文成績和使用次數為中度相關,且無顯著性。
由上可知,有無控制變數的加入,對結果可能會有不同的影響,因此在分析時研究者需要對於控制變數多加考量。
四、結論
本研究採用Pearson偏相關分析判斷「在控制智力時,英文成績和使用次數是否有關」。已知兩個變數均為連續變數,透過散佈圖顯示兩變數之間呈線性關係,箱型圖顯示兩變數的資料無異常值,且Q-Q圖和Shapiro-Wilk檢驗顯示資料為常態分佈。
Pearson偏相關分析結果顯示,英文成績和使用次數之間呈正相關,且無顯著性。即表示控制智力後,英文與使用次數沒有關係。


封面圖-500x383.png)


