路徑分析用於探討構面與構面之間的關係,以下將詳細說明其原理。
一、使用情形及說明
結構方程模型 (SEM) 由兩個部分所組成, 第一部分是測量模型 (measurement model),了解每個潛在變數下的結構是否符合理論預期?會以驗證性因素分析 (CFA)來分析;另一個則為結構模型(structural model),探討研究者提出的特定行為科學理論,其變數間複雜的因果路徑關係,因此也稱為路徑分析(Path analysis, 以下簡稱 PA)。上回 CFA 已經探討了前者,本篇要探討的觀念與實作則是第二部分結構模型的部分。
二、觀念簡介
1921 年,美國遺傳學者 Sewell Wright 首先提ft了路徑分析(PA)的概念, 用以處理演化與突變的機制關係。之後路徑分析受到許多社會科學領域的採用,不管是經濟學,心理學,甚至教育與政治學。其實,路徑分析可以說是結構方程 模型(SEM)的一種特殊的亞型,只要把 PA 看為每個變數都只用一個可觀察指標 (observable indicator)來測量的 SEM 即可。換言之,PA 不是只有一條迴 歸式,而是用一組迴歸式來同時估計效果的模型,對於行為科學複雜的理論建構, 以及理論上因果關係爭議(例如到底是動機影響了成績,還是成績影響了動機, 抑或是兩者互為因果?)的釐清很有幫助。
路徑分析(PA)常常用以處理中介效 果(mediated effect)的分析。中介模型(mediated model)為行為科學領域用來驗證因果機制(causal mechanism)。
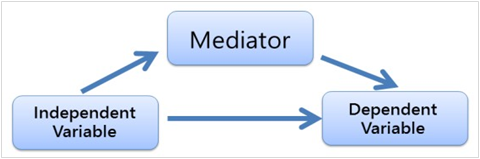
以上圖為例,研究者初期已經建立了自變數與依變數之間的關係,但是想進一步理解,自變數到底是透過甚麼機制來影響依變數。
舉例而言,一家企業的 HR 部門發現舉辦某個 training program 後,參與員工的工作績效顯著提升了。對於 HR 主管而言,他(她)或許有興趣於到底是甚麼樣的因果機制導致了這樣的效果?因 此其作了一些假設,並在下一次施行時,測量那些變數,結果發現是因為 training program 提升了員工的自我效能感,進而使其願意挑戰自己,而讓工作績效隨 之爬升。在這裡,自我效能感就是中介變數,從這次的分析中,可以讓該組織了 解到,之後不管有沒有該 training program,透過各種途徑與方法提升員工的 自我效能感才是真正核心的關鍵,因為這能讓員工工作績效更上一層樓,進而讓 整體組織都能獲益。
在上圖中,自變數本身對於依變數的獨特效果,稱為直接效 果(direct effect);而自變數透過中介變數(mediator)影響依變數的部分,則稱 為間接效果(indirect effect),兩種效果加總,就是所謂的總效果(total effect)。 在方法論上,模型考量了中介變數後,若直接效果變得不顯著,表示該中介變數有完全中介(complete mediation)的效果,但只是讓直接效果的估計值變小, 但仍然具有統計顯著性,稱為部分中介(partial mediation)效果,以 training program 為例,表示很可能除了自我效能感外,還有其他心理因素也中介了該 program 對於工作績效的關係,進一步探究以便釐清。
三、R軟體實務操作
介紹了基礎的中介模型與路徑分析的概念後,接著我們利用一些公開的資料 檔 來 做 實 際 的 分 析 。 UCLA 的 Institute for Digital Research and Education(IDRE)有提供 SAS 檔案,因為我們利用 R language 做示範,因此先 下 載 可 以 讀 取 SAS 數 據 檔 的 package: sas7bdat :
當然,就跟所有 package 一樣,使用時都得用 library 將其載入: 接著,將該網址內的數據檔讀入 R,並存在 path.data 這個變數中(該變數可自行取名),接著,因為要執行路徑分析,因此我們將 lavaan 該 package 載 入。
輸入path.data<-read.sas7bdat(“http://www.ats.ucla.edu/stat/data/hsb2.sas7bdat”)
library(lavaan) -套用lavaan這個package
載入數據後,我們一般會動用 names( )函數來檢視該數據內有那些變數:
輸入names(path.data)

最終讓科學(science)領域的能力被加強?很明顯數學(math)在此理論假設中,可以看到裡面有樣本的 id,性別,族裔,社經地位,學校型態等人口學變數外,剩下的就是其在各學科的數據,例如閱讀,寫作,數學,科學,社會等科 目。假如某教育研究者欲了解閱讀(read)的能力是否會透過提升數學(math)能力,
就是扮演著中介變數的角色,模型設定如下:

破折號左邊的是內Th變數或依變數,右邊的則是外Th變數或自變數。#後面 到換行前都是附註,那邊的程式碼將不會被執行。從這邊的 R code 可以觀察到, 我們先用 read 對 science 做迴歸,估計直接效果;同理可證,接著用 read 去 對 math 作迴歸,以及 math 對 science 對迴歸,兩者的係數估計值相乘後是為間接效果,亦稱為中介效果。

接著,調用 sem( )函數來執行分析,將其存入 fit 變數後,然後用 summary( ) 函數要求 R 給我們詳細的模型估計資訊。其中 standardized=T 會回傳標準化的 迴歸係數,rsq=T 則會給我們模型的解釋力。
四、結果解釋
由下面的報表中可以看到,每一條路徑都達到統計上的顯著水準(p < .000), 且係數都是正值,這意味著
1. 在考量了數學成績後,閱讀成績愈優秀者,科學成績一般也比較好。(direct effect)
2. 閱讀成績愈好者,其數學成績也會相應水漲船高。
這些結果其實蠻合理的,因為如果對於文字的理解無法掌握好,那麼可能解題時會遇到困難。而數學成績愈
好者,科學成績平均而言也會較高,這點也符合我們一般人的認知。
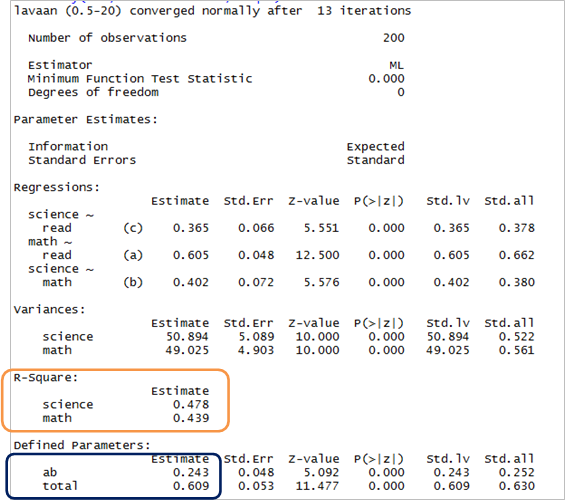
而橘色框框的部分則是每個內Th變數被解釋的變異百分比,分別 都有 4 成以上的解釋力。靛色框框的部分則是 mediated effect(ab 交乘項,也 就是間接效果),以及總效果。由於控制了中介變數後,直接效果(報表中 c 的估 計值)仍是顯著的,因此數學成績僅有部分中介的效果,仍有部分的效果是直接 來自閱讀能力,或者可能還存在其他的中介變數會影響科學的成績或能力。由於我們有要求 R 給ft標準化迴歸係數,即 std.lv。該欄位跟 Estimate 欄 位(非標準化係數)的數值是一致的,因為我們的數據已經經過標準化後才丟入模 型去分析所致。
本範例用一個單純的中介模型來介紹路徑分析,當然,隨著理論的漸趨複雜,模型的設定也會隨之愈來愈精緻,但基本邏輯與 R 語言的寫法並無二致,lavaan 這個 package 給予相關研究或實務工作者一個很強大的工具來進行這方面的分 析。尤其對於很多因果關係的爭議而言(到底是誰影響誰?又是透過甚麼路徑影 響?),分別建模後,看看何者的模型配適較佳,或許對於許多爭辯有著止息的 效果存在。
值得注意的是,路徑分析跟之後要介紹的結構方程模型基本上資料來 源仍是 observational data,因此在因果推論上仍需謹慎。


封面圖-500x383.png)


