皮爾森相關分析用於探討兩變數之間的線性關係,其值介於-1~1之間,以下將詳細說明其原理及SPSS操作。
一、使用狀況:
皮爾森相關分析用於探討兩連續變數(X, Y)之間的線性相關,若兩變數之間的相關係數絕對值較大,則表示彼此相互共變的程度較大。一般而言,若兩變數之間為正相關,則當X提升時,Y也會隨之提升;反之,若兩變數之間為負相關,則當X提升時,Y會隨之下降。
皮爾森相關係數公式為:
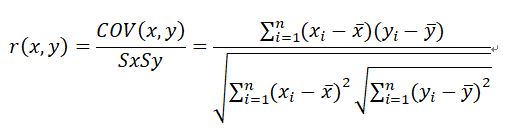
![]()
*【小常識】
1、皮爾森相關分析並無法確切偵測到非線性的相關,例如指數或對數的相關,此時要先將變數進行轉換,再進行相關分析。
2、相關分析並無法直接做出因果推論,因果推論必須要符合變數的獨立性、時序性及相關性,通常也需要參考文獻的邏輯推導過程,單純由相關分析是不足以直接斷定變數之間的因果關係的。
二、假說檢定
虛無假說(Null hypothesis)→ H0 : r = 0 兩變項之間無顯著相關
對立假說(alternative hypothesis)→ H1 : r≠ 0 兩變項之間有顯著相關
三、SPSS 操作範例
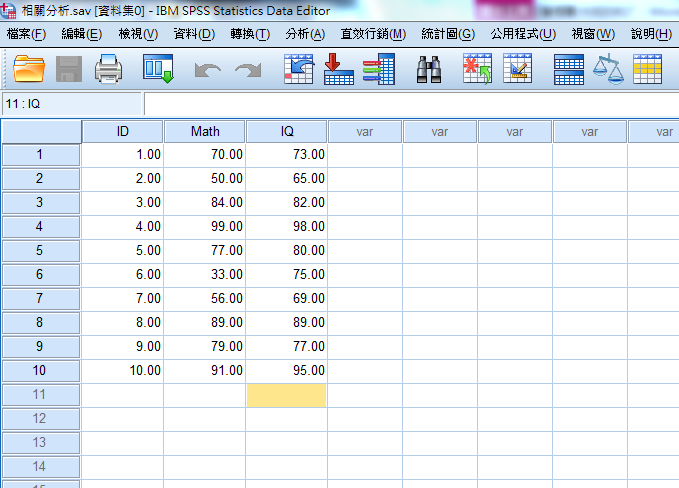
(一)輸入SPSS資料
資料中ID為學生編號,Math為數學成績,IQ為學生智商分數。
(二)散佈圖(Scatter plot)
在進行相關分析之前,建議研究者先進行散佈圖的繪製,可以確認兩變數之間是否有線性以外的關係。
統計圖->歷史對話紀錄->散佈圖->簡單散佈圖
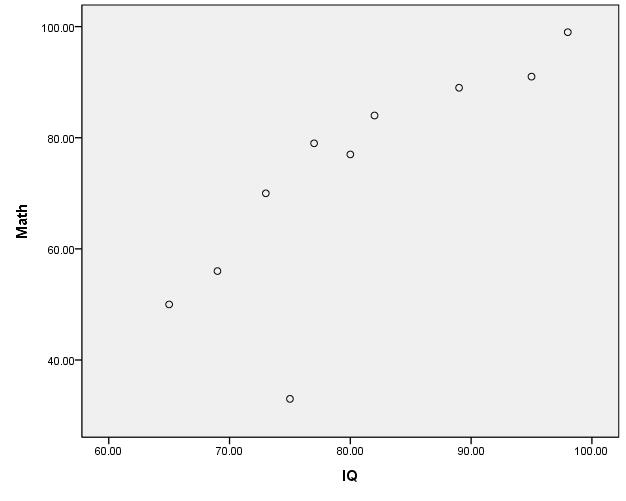
將Y軸輸入Math資料,X軸輸入IQ資料
由圖可知,Math跟IQ之間可能有線性關聯,較不像有其他非線性的關係,確認之後接著進行相關分析。
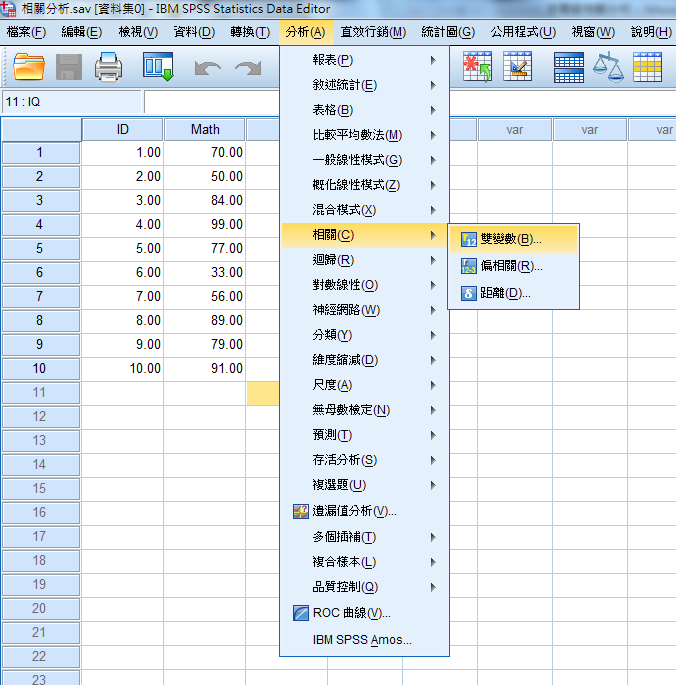
(三)分析->相關->雙變數
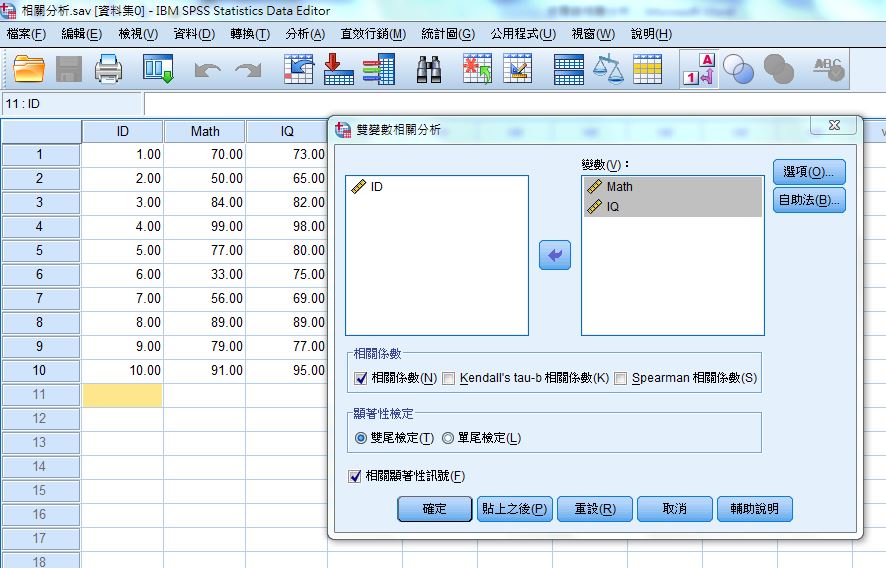
將要探討的變數拉進變數的框框內,按下確定即可。
(四)報表解讀
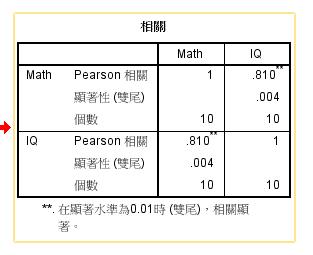
相關係數報表顯示,Math與IQ之間的關聯為0.810,顯著性為0.004,兩者達到顯著的正相關,表示兩者之間彼此會正向共變。一般的研究者可能會根據文獻推斷,IQ越高的人,數學成績也會越高。
補充:一般研究者認為,相關係數0.3以下為低相關,0.3~0.7為中等相關,0.7以上為高度相關,故本研究結果可推定兩變數之間為高度相關(黃姵嫙,2018)。
本研究範例資料可從以下連結取得,僅供同學練習使用:
參考文獻
黃姵嫙(2018)。綠色招募活動對組織人才吸引力之影響:以個人組織配適知覺為中介變數與個人環保態度為干擾變數(未出版之碩士論文)。東海大學,台中市。


封面圖-500x383.png)


