研究者在發展一個新的構念(construct)時,會依據這個新構念的定義,依據歸納法的流程,編制適合且具代表性的題目,形成新的測量工具,而此新量表需要具備良好的信效度。
此外,若為應用在臨床上篩檢的量表,則需另外找出關鍵的切截點分數(cut-off score),找出正確篩檢出高風險族群的分析,此時就需要進行「ROC曲線法(ROC curve, receiver operating characteristic curve)」(以下均簡稱為ROC)的分析。
接下來,本篇文章會介紹ROC的基本概念,以及提供一個範例,使用SPSS統計分析軟體進行ROC分析的操作,並在最後解說如何判讀最佳的切截點分數。
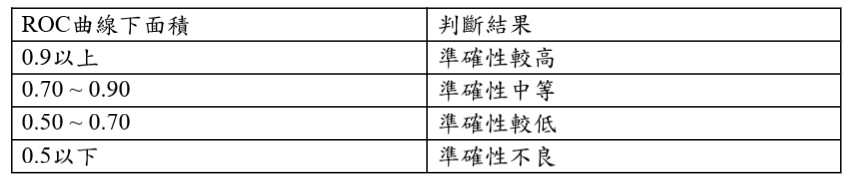
ROC分析會提供ROC 曲線下面積(area under the ROC curve, AUC),其功能在於告訴我們這個新量表具備多準確的篩檢能力,roc曲線下面積越大,表示新量表篩檢的準確度越高,以下表格為詳細的判斷標準依據。
表1 ROC曲線下面積的判斷標準
參考文獻:蘇宜芬、張祐瑄、李孟峰、黃鈺茜(2016)。國小二至六年級朗讀流暢度篩檢準確度及切截點分析。教育科學研究期刊,61(4),33-57。doi:10.6209/JORIES.2016.61(4).02
如果已經確認新量表的曲線下面積具有良好的篩檢度之後,下一步就是介紹ROC曲線的橫軸和縱軸標題。
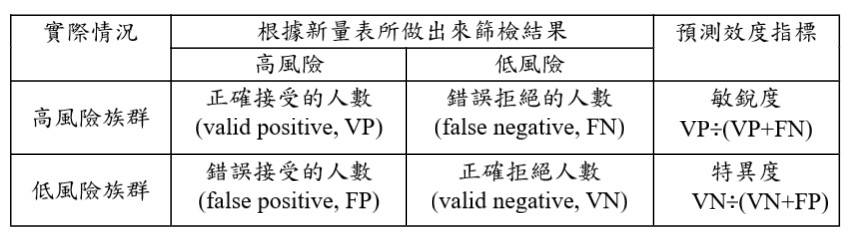
- 橫軸為「錯誤接受率」:
- 被錯誤篩檢出為高風險個案的人數占所有低風險個案人數的比率。
- 為1-特異度:「FP÷(FP+VN)」
- 縱軸為「正確接受率」:
- 正確地篩檢出高風險個案的人數占所有高風險個案人數的比率。
- 例如100個人當中,有40個人是高風險個案,而用新量表某個切截點分數可篩檢出30個人是高風險個案,其正確接受率為30/40 = 0.75。
- 為敏銳度:「VP÷(VP+FN)」
- 命中率
- 正確接受和正確拒絕的個案人數佔整體篩檢人數的比率。
- 計算公式為:「(VP+VN)÷(VP+FN+FP+VN)」
- 錯誤拒絕率
- 高風險個案未被篩檢人數占所有高風險個案人數的比率。
- 計算公式為:「FN÷(VP+FN)」
表2 預測校標各項指標
參考文獻:蘇宜芬、張祐瑄、李孟峰、黃鈺茜(2016)。國小二至六年級朗讀流暢度篩檢準確度及切截點分析。教育科學研究期刊,61(4),33-57。doi:10.6209/JORIES.2016.61(4).02
【範例】
檢測青少年憂鬱量表的切截點分數(cut-off score),校標採用貝克憂慮量表(The Beck Depression Inventory, BDI)
【SPSS分析過程與結果】
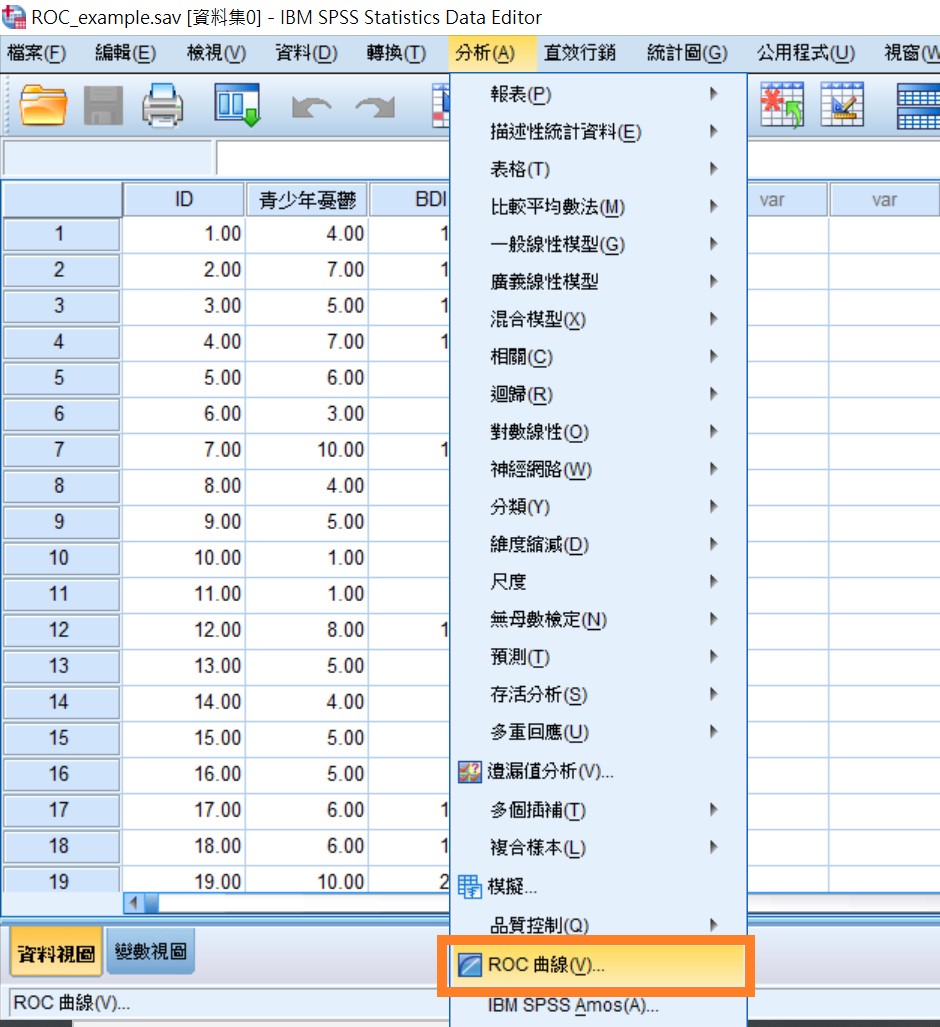
一、載入資料
SPSS的「分析」→「ROC曲線」
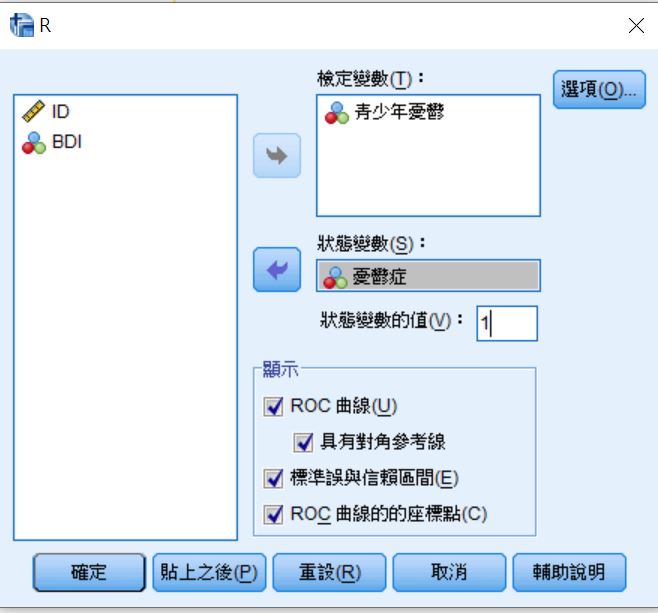
二、設定變數
將青少年憂鬱量表放入「檢定變數」,將症狀放入「狀態變數」,並需要輸入症狀的判定編碼。
本篇範例將憂鬱症之個案編碼為1 (BDI>=10),因此在狀態變數的值輸入1。
三、分析結果
本研究發現AUC(曲面下面積)為0.905,高於0.7的標準,且檢定顯著性小於0.05,表示青少年憂鬱量表在預測症狀上有顯著效果。
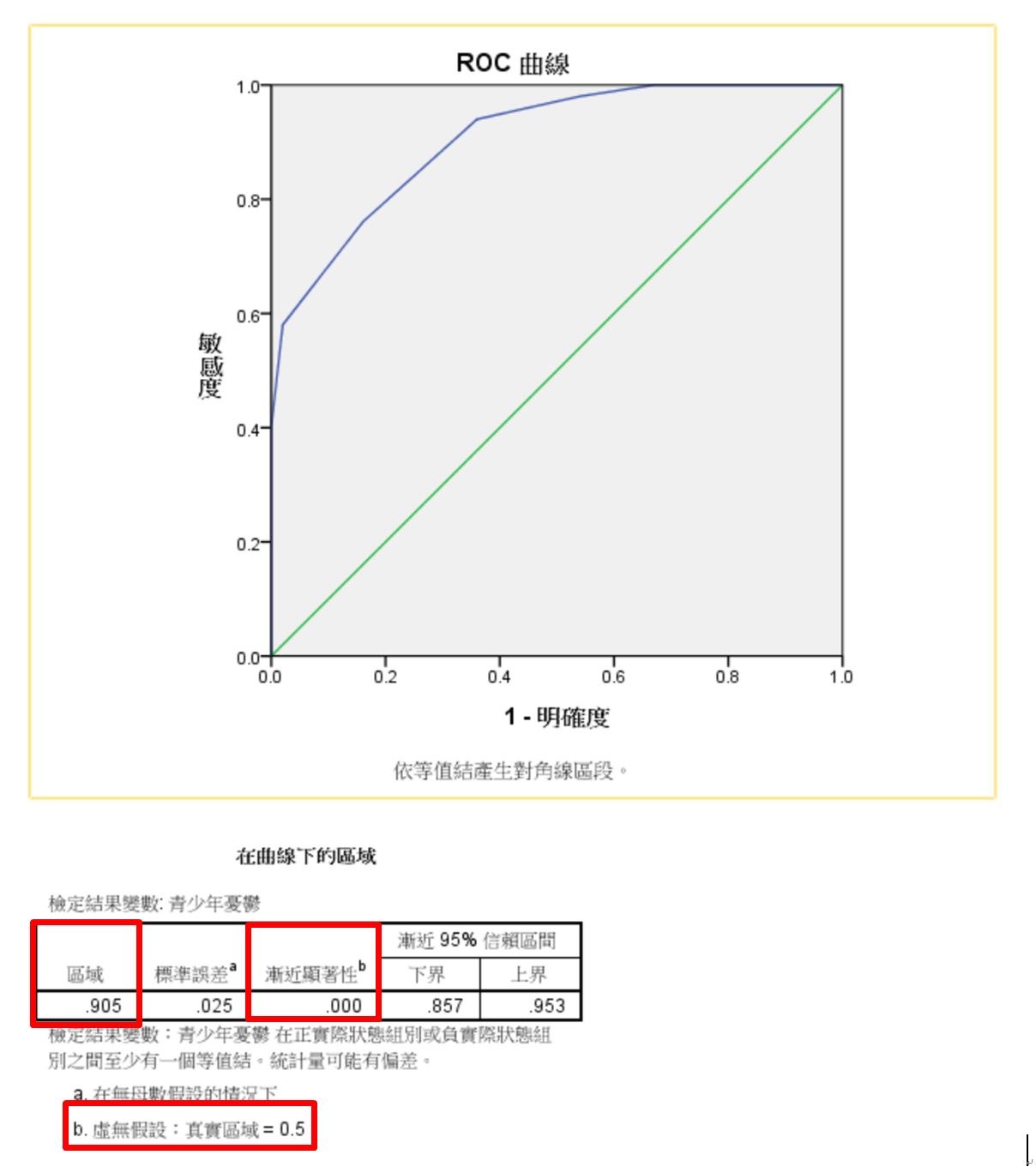
因為SPSS的中文版有許多翻譯問題,所以這邊的1-明確度為上述提及之「1-特異度」。
下述資料可以用於判斷最佳切點,根據Youden index = 敏感性(sensitivity)+特殊性(specificity)進行判定。
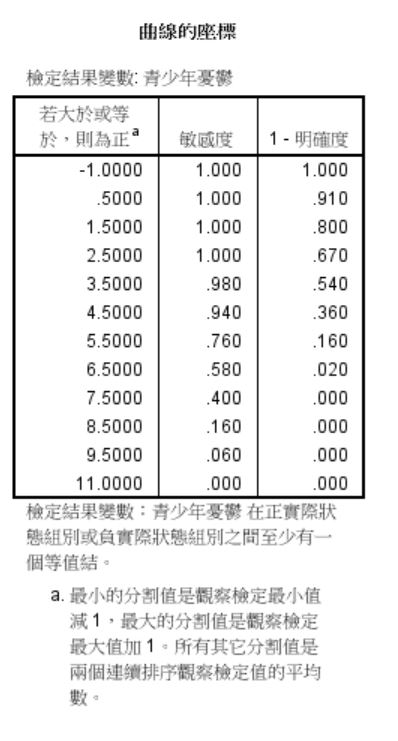
四、【切截點分數判斷標準】
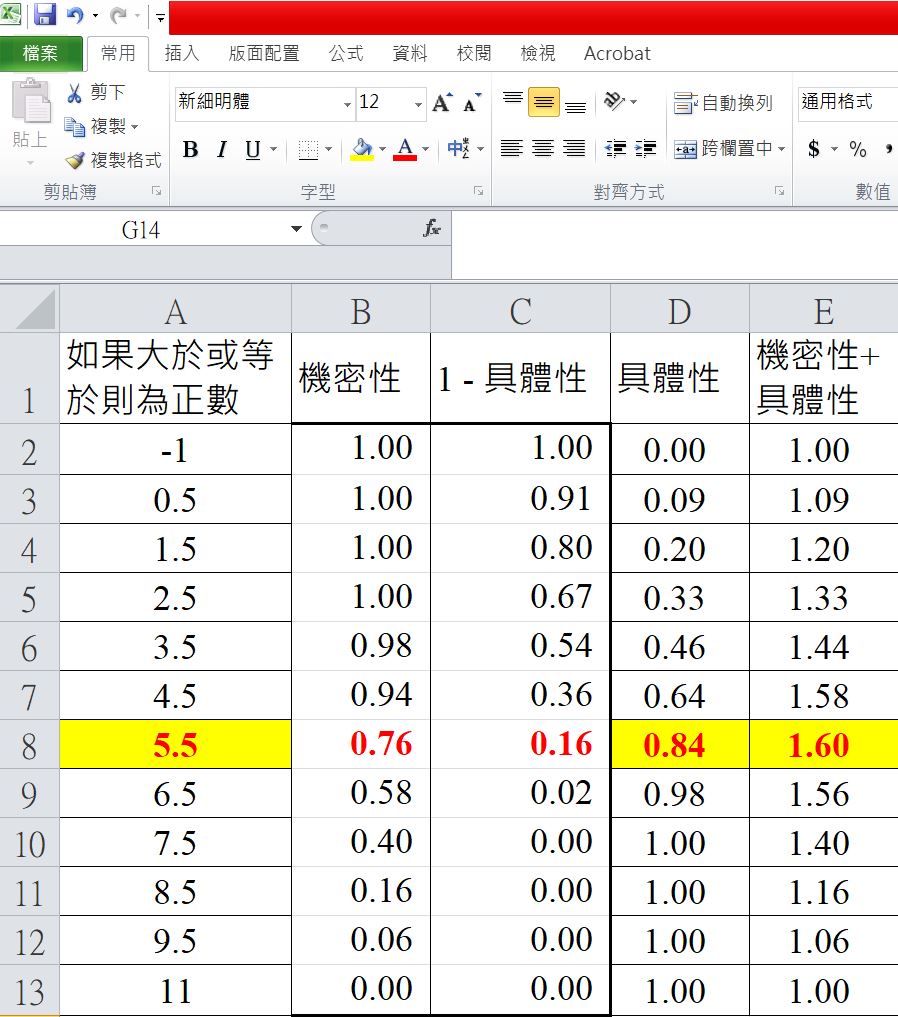
最常使用作為切截點分數的判斷依據為「敏感性(sensitivity)+特殊性(specificity)」後得分最高者,即為最適的切截點分數(林方琳、林月仙,2012)。
下圖顯示青少年憂鬱量表的最適切截點分數為「5.5分」。
【參考文獻】
林方琳、林月仙(2012)。「學前兒童疑問句回應測驗」之編製。測驗學刊,59(2),187-218。doi:10.7108/PT.201206.0187
蘇宜芬、張祐瑄、李孟峰、黃鈺茜(2016)。國小二至六年級朗讀流暢度篩檢準確度及切截點分析。教育科學研究期刊,61(4),33-57。doi:10.6209/JORIES.2016.61(4).02


封面圖-500x383.png)


