簡單線性迴歸分析用於探討單一自變數及依變數(連續變數)之間的關係,本章將仔細說明其使用方式及SPSS範例推演。
一、使用狀況
迴歸 (regression) 方法是一個分析變數和變數之間關係的工具,主要在探討自變數(x)與依變數(y)之間的線性關係,透過迴歸模型的建立,可以推論和預測研究者感興趣的變數(y)。
簡單線性迴歸: 利用單一自變數(x)去預測一個依變數(y)。
二、前提假設
1.假設模型:
其估計式為:Y=B0+B1X1
2.誤差項需滿足三大假設:
(1)常態性(Normality) : 若母體資料呈現常態分配(Normal Distribution),則誤差項也會呈現同樣的分配。可採用常態機率圖(normal probability plot) 或Shapiro-Wilk常態性檢定做檢查。
(2)獨立性(Independency) : 誤差項之間應該要相互獨立,否則在估計迴歸參數時會降低統計的檢定力。我們可以藉由Durbin-Watson test來檢查。
(3)變異數同質性(Constant Variance) : 變異數若不相等會導致自變數無法有效估計依變數。我們可以藉由殘差圖(Residual Plot)來檢查。
三、假說檢定(Hypothesis Testing)
1. 迴歸模型的顯著性檢定(F test): 探討迴歸模型中的β係數是否全部為0。
當係數不為0時,迴歸模型才具有預測力。
虛無假說(Null hypothesis)→β1=β2=βn=0
對立假說(alternative hypothesis)→至少有一個β不為0
統計值(Statistics)→F
2. 個別迴歸係數的邊際檢定(t test):探討個別自變數之β係數是否為0。
當係數不為0時,自變數才具有解釋力。
虛無假說(Null hypothesis)→βn係數為0
對立假說(alternative hypothesis)→βn係數不為0
統計值(Statistics)→t
*【小常識】
在簡單線性迴歸中,F test和t test的統計意義相同。
判定係數: 迴歸模型的總變異中可被自變數解釋之百分比, 判定係數越大迴歸模型的配適度越好。一般而言,判定係數大於0.5就算不錯了。
四、SPSS 操作Example
【例題】由公司的廣告支出去預測其銷售額。
本題例子為簡單線性迴歸,以一個x(廣告支出)去預測y(銷售額)。
1. 在SPSS中輸入欲分析之資料。
本次範例中,以廣告為自變數,y為依變數。
2. 簡單線性迴歸:分析→迴歸→線性
3. 因變數:銷售額(y)
自變數:廣告費(x)
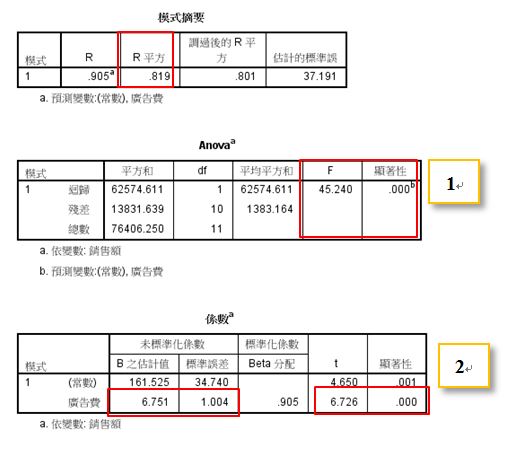
4. 檢定結果:
(1)迴歸模型的顯著性檢定(F test):
在本例中,計算後的F統計值為45.24,顯著性p值<0.001,拒絕虛無假說。
→此迴歸模型顯著,具有預測能力。
(2)個別迴歸係數的邊際檢定(t test):
在本例中,計算後的t統計值為6.726,顯著性p值<0.001,拒絕虛無假說。
5. 檢定誤差是否滿足三大假設:
(1) 常態性
A、分析→迴歸→線性→儲存→殘差未標準化
B、分析完後在原始資料的最後一行出現未標準化殘差:RES_1
C、得到殘差數值之後,接著進行殘差的常態分析→描述性統計資料→探索
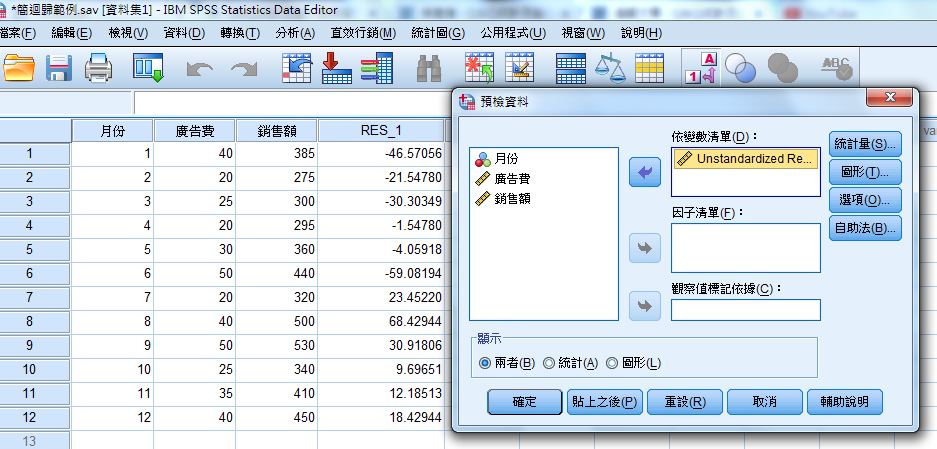
D、放入依變數(殘差):Unstandardized Residual
E、勾選圖形→常態機率圖附檢定
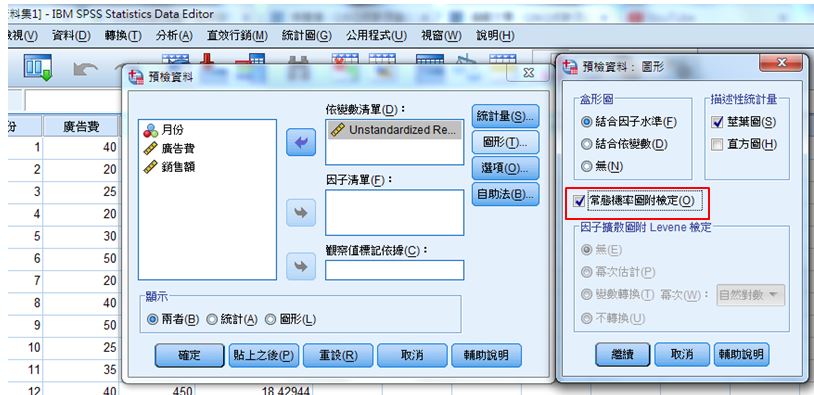
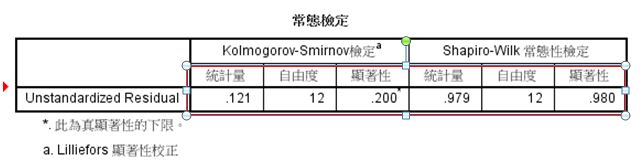
F、使用Shapiro-Wilk常態性檢定,H0:常態 V.S. Ha:非常態。顯著性=0.98>0.05,不拒絕H0,表示殘差分佈為常態,迴歸模型的常態性通過。
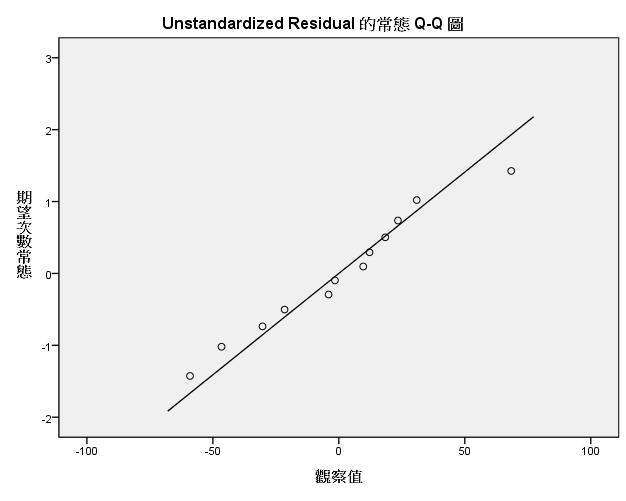
另外,根據常態機率圖的特性,若殘差成45度線則服從常態。根據上圖,我們發現本模型的殘差近似於一條45度的直線,因此也能推論其服從常態性的假設。
接著以下探討第二個假設,獨立性。
(2) 獨立性
A、分析→迴歸→線性→統計資料→Durbin-Watson
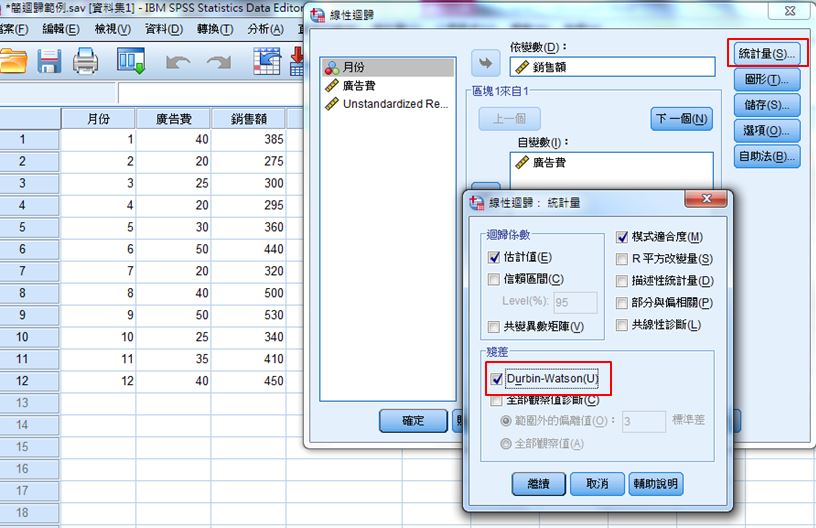
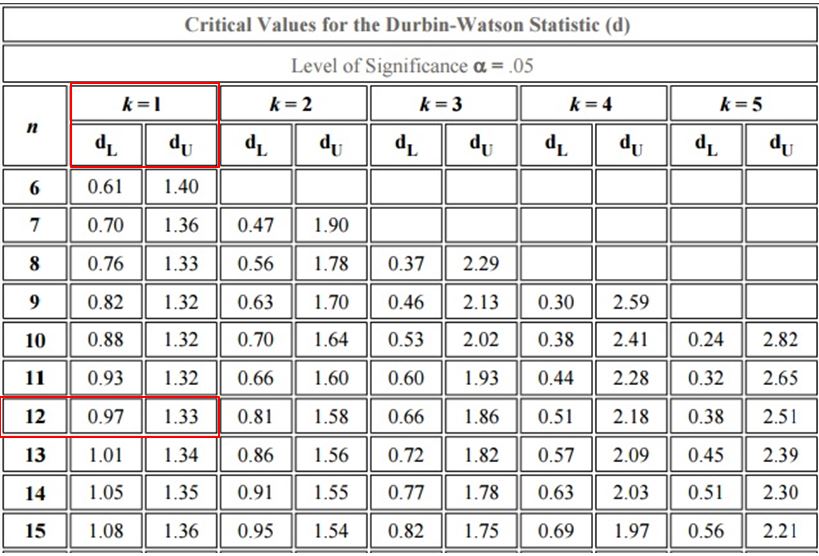
B、◆判斷準則:若Durbin-Watson 值<DL 表示資料不獨立
若Durbin-Watson 值>DU 表示資料獨立
若DL <Durbin-Watson 值< DU 則無結論
(K=1:只有一個自變數)
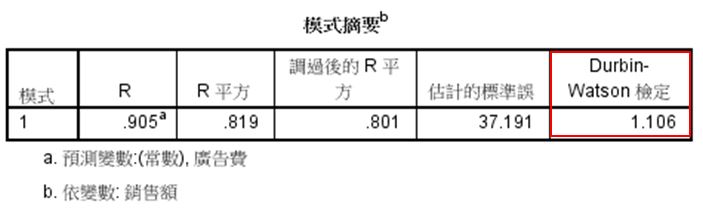
C、利用查表看資料是否具獨立性,因為Durbin-Watson 值=1.106,介於DL和DU之間,所以無法判定。
*【小常識】
DW值愈接近2,代表其愈獨立。
(3) 變異數同質性
A、分析→迴歸→線性→圖形→Y:*ZRESID,X:*ZPRED
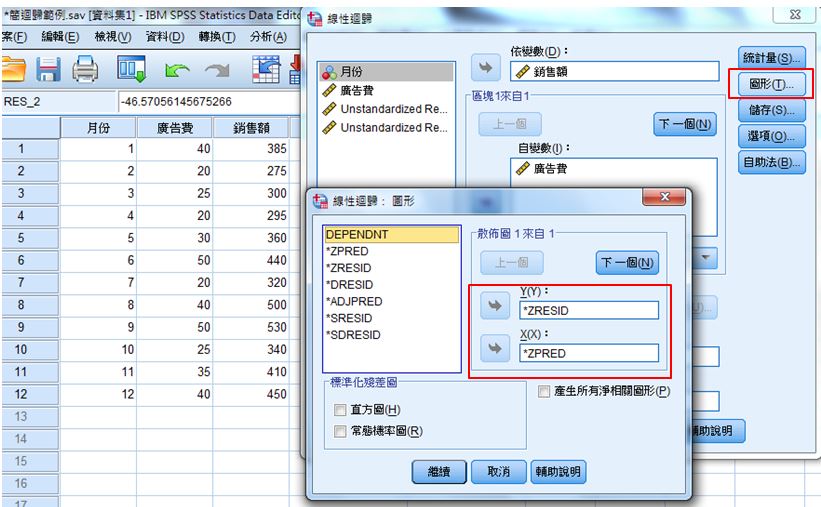
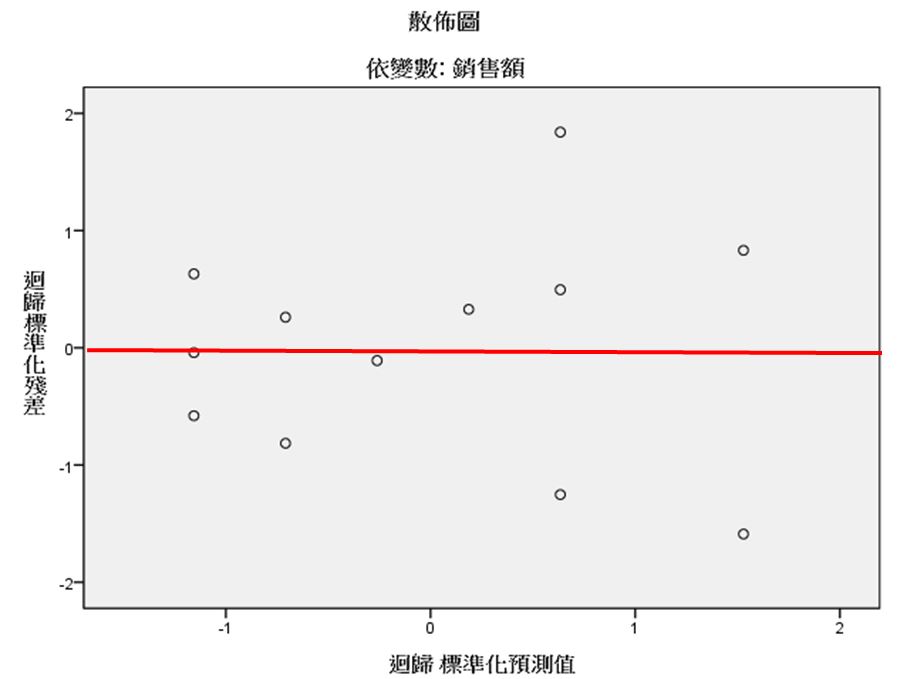
B、我們從標準化殘差和預測值的散佈圖中,可以發現資料大致上沿著0線上下均勻跳動,因此符合變異數同質性的假設。
以上為簡單迴歸的基礎說明,後續同學可以參考多元迴歸分析以了解更深入的應用。
本次教學範例檔如下所示,僅供同學練習使用:


封面圖-500x383.png)


