本篇文章主要說明虛擬變數的功用和如何使用STATA生成虛擬變數。在常見的迴歸分析中,自變項通常是連續變項,因為迴歸分析假設自變項與依變項存在著線性關係。若自變項並非等距或比率變項,而是類別變項時,就需要先產生虛擬變數(dummy variable),而這時就需要生成虛擬變數的語法了。下述的操作說明將針對虛擬變數進行詳細說明。
一、二元類別(類別變數為2類,以0、1變數進行分析)
首先舉例而言,一個簡單迴歸方程式 Y=B0+B1X,其中Y為依變項,X為自變項,B0與B1是經迴歸分析所估計出來的係數,而B1說明了X與Y之間的關係,即每當X增加1,Y就會增加B1。
那如果想要用類別而不是連續的變項來估測Y呢?如果X為自變項,例如性別、父親籍貫等,方程式 Y=B0+B1*性別,此時若解釋成每當性別增加1,依變項會增加B1,但是性別屬於類別變項,何來增減的程度差異呢?又如果類別變項有三類以上呢?難道能說父親籍貫每增加1,依變項就會隨之增加B1嗎?
想要正確解釋類別變項在迴歸方程式中的意義,就應該先產生一種新的變數:虛擬變數(dummy variable)。因應類別變項不能放進迴歸模型中檢測,所以設定1、0的數字來建立虛擬變項,例如在性別變項中,將男性設1,女性設0,如此一來便能計算出平均數等數值,也能放進迴歸模型裡跑檢定值。
在STATA中設立虛擬變數的方式為:
gen sex_d1 =sex; (生成新的虛擬變數稱為sex_d1)
recode sex_d1 1=1 2=0; (將男性設為1,女性設為0)
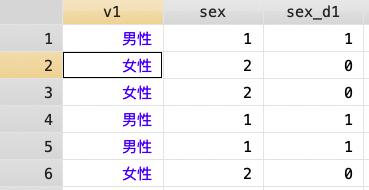
如今男性的虛擬編碼為1,女性的虛擬編碼為0,在迴歸方程式中只需放入sex_d1作為自變項即可,只要sex_d1為1就是指男性,sex_d1為0的話就是女性。
假設有一個迴歸模型是分析主觀社會地位和性別間的關係,如下圖:
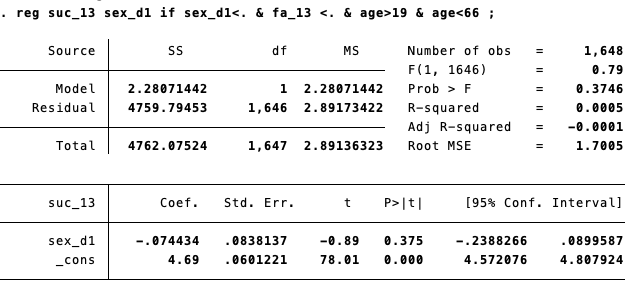
這組模型的迴歸方程式為: y=4.69-0.074*B。其中y是主觀社會地位,而B是男性,男性受訪者的編碼為1,女性受訪者的編碼為0。分別將1與0代回方程式時:
男性的「主觀社會地位」(y)平均數=4.69-0.074×1=4.616,
女性的「主觀社會地位」(y)平均數=4.69-0.074×0=4.69, (女性的y平均數=截距,也就是上圖的「_cons」即「constant」)
男性的主觀社會地位-女性的主觀社會地位=-0.074分,即迴歸係數B,B為兩性主觀社會地位的平均數差異情形。迴歸係數B是以編碼為1的對象平均數減去編碼為0的對象,因此在若有顯著的情況下,可將虛擬變項的迴歸係數,解釋為男性(編碼1群體)相對於女性(編碼0群體)有比較低(因迴歸係數為負)的主觀社會地位。
二、多元類別(類別為3類以上)
當類別數變成4組,比方說父親籍貫為台灣閩南人、客家人、原住民、大陸各省市共四組,在STATA中設立虛擬變數為:
gen fa_d1= fa_13; (生成新的虛擬變數稱為fa_d1)
recode fa_d1 1=1 2=0 3=0 4=0; (將台灣閩南人設為1,其他設為0)
gen fa_d2= fa_13; (生成新的虛擬變數稱為fa_d2)
recode fa_d2 1=0 2=1 3=0 4=0; (將客家人設為1,其他設為0)
gen fa_d3= fa_13; (生成新的虛擬變數稱為fa_d3)
recode fa_d3 1=0 2=0 3=1 4=0; (將原住民設為1,其他設為0)
gen fa_d4= fa_13; (生成新的虛擬變數稱為fa_d4)
recode fa_d4 1=0 2=0 3=0 4=1; (將大陸各省市設為1,其他設為0)

雖然生成了四個虛擬變數,但是迴歸方程式只需放入三組虛擬變數(fa_d2、fa_d3、fa_d4)自變項即可,因為只要其中三組都是0,就可以回推隱藏的那一個參照組(fa_d1)是1。研究者可依據自身的研究需求去決定參照組為何,藉以確認用以比較的組別符合研究的需求。迴歸模型示範如下圖:
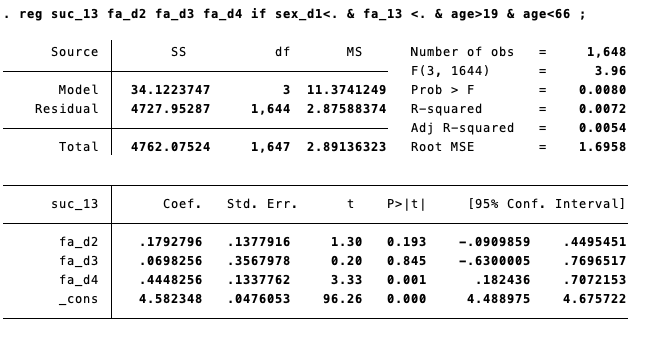
依據上方迴歸模型的係數(Coef.),主觀社會地位(y)和籍貫(B)間的迴歸方程式為 y=4.582+0.179*B1+0.070*B2+0.445*B3,虛擬變項編碼都為0的那組(台灣閩南人)視為參考組,將1、0代入方程式的結果如下:
父親為台灣閩南人的平均主觀社會地位=4.582+0.179×0+0.070×0+0.445×0=4.582 (參考組的依變項平均數=截距 constant)
父親為台灣客家人的平均主觀社會地位=4.582+0.179×1+0.070×0+0.445×0=4.761
父親為台灣原住民的平均主觀社會地位=4.582+0.179×0+0.070×1+0.445×0=4.652
父親來自大陸各省市的平均主觀社會地位=4.582+0.179×0+0.070×0+0.445×1=5.027
另一方面,若有顯著的情況下,也可推論迴歸係數>0的組別,相對於參考組有更高的主觀社會地位。不過在上圖的模型中只有fa_d4呈顯著,因此只能說B3=1的那組(大陸各省市)相對於參考組(台灣閩南人)有更高的主觀社會地位(B=0.445, p<.05)。


封面圖-500x383.png)


