二因子變異數分析用於探討兩變數在依變數上的影響,本文以獨立樣本為例,故分析方法為二因子獨立變異數分析。
一、使用狀況:
比較多組(兩組以上)樣本平均數是否相等。
變異數分析是用來檢定多組樣本平均數是否相等,並非在檢定變異數。
雙因子變異數分析(Two-way ANOVA):有兩個自變項的變異數分析。
獨立樣本(Independent Sample):比較青年、中年、老年三個年齡層的族群,對於飲料甜度的喜好以及每日總攝取糖分量是否不同。
二、前提假設:
(一)依變項(Dependent variable):
(1)必須是連續變數(continuous variable)
(2)必須為隨機樣本(Random variable)→從母群體(Population)中隨機抽樣得到
(二)依變項的母群體:必須是常態分佈(Normal Distribution)
(三)獨立事件(Independent event):
樣本須為獨立變項(Independent variable)→第一組的樣本不影響第二組的樣本;第二組的樣本也不影響第一組。
例如:分析從日本、美國兩地進口的水果(蘋果、香蕉、西瓜)與台灣當地的水果甜度是否有差異,從日本或美國進口與台灣當地的水果這三組樣本量測不會互相影響
(四)變異數(Variance)同質性:各組樣本間變異數必須相等。

*【小常識】
重複量測變異數分析→當樣本不是獨立事件時
單因子變異數分析→當樣本只有一個自變項時
三、假說檢定(Hypothesis Testing):
分析前先考慮三個問題:
(一)兩因子間是否有交互作用?
交互作用表示不同因子在依變數上的差異達顯著,意即兩因子間會相互影響。
(二)因子A處理間平均數是否相等?
虛無假說(Null hypothesis)→因子A各組間平均數相等
對立假說(alternative hypothesis)→因子A中至少兩組平均數不相等
統計值(Statistics)→ F=MSA/MSE, F值愈大→組間(相對於組內)差異愈大
(三)因子B處理間平均數是否相等?
虛無假說(Null hypothesis)→因子B各組間平均數相等
對立假說(alternative hypothesis)→因子B中至少兩組平均數不相等
總變異量 = 因子A處理間的變異量 + 因子B處理間的變異量 + 交互作用+殘差
(可解釋的差異) (不可解釋的差異)
總自由度 = 因子A處理間的自由度 + 因子B處理間的自由度 +交互作用+ 殘差的自由度
→ N-1 = (r-1) + (c-1) + (r-1)(c-1)+rc(n-1)
| 離均差平方和(SS) | 自由度(DF) | 均方和(MS) | F (檢定) | P (顯著) | |
| 因子A | SSA (組間變異) | DFA=r-1 (組別-1) | MSA | MSA/MSE | 查表 |
| 因子B | SSB (組間變異) | DFB=c-1 (組別-1) | MSB | MSB/MSE | 查表 |
| 因子A*B | SSE (交互作用) | DFE=(r-1) (c-1) | MSA*B | ||
| 全體 | SST (總變異) | DFT=N-1 (樣本數-1) |
(四)二因子ANOVA統計公式

四、SPSS 教學範例 Example:
【例題】比較三種廣告方式(A, B, C)在五個不同廣告時段(I, II, III, IV, V),所達成的廣告銷售額是否不同?
本題的例子為兩個觀察因子(廣告方式、廣告時段),故選擇Two-Way ANOVA檢測樣本的平均值是否不同
(一)試問廣告方式是否影響產品銷售額?
虛無假說(Null hypothesis)→廣告方式不會影響銷售額
對立假說(alternative hypothesis)→廣告方式會影響銷售額
(二)試問廣告時段是否影響產品銷售額?
虛無假說(Null hypothesis)→廣告時段不會影響銷售額
對立假說(alternative hypothesis)→廣告時段會影響銷售額
(三)操作步驟
1. 在SPSS中輸入欲分析之資料。
Total sale為總銷售額,Method為廣告方式,Time為廣告時段,AD為編號(分析用不到)。
2. Two-Way ANOVA:分析→一般線性模式→單變量
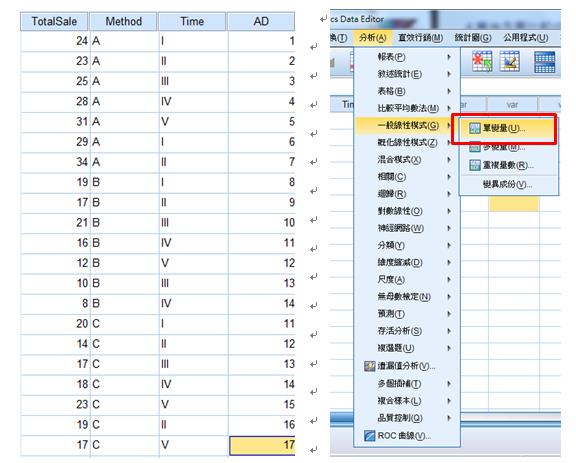
3.依變數:產品銷售額(Sale)
因子A:廣告方式(Method)
因子B:廣告時段(Time)
Post Hoc檢定:可選擇欲呈現的事後檢定的方式
選項:可選擇需要的統計檢定資訊
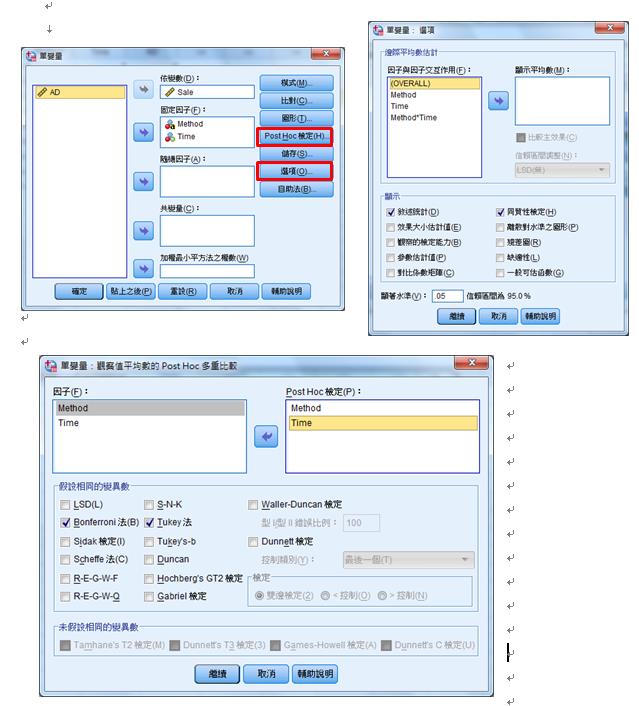
4.檢定結果:
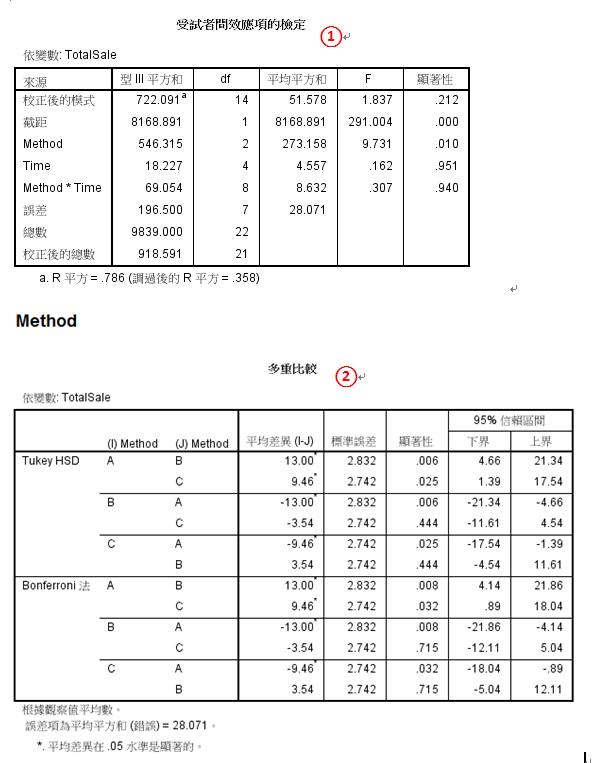
(1二因子變異數分析:
在本例中,計算後的廣告方式之F統計值為9.731,顯著性p值=0.010<0.05,拒絕虛無假說。
廣告時段之F統計值為0.162,顯著性p值=0.951>0.05,無法拒絕虛無假說。
→不同廣告方式對廣告銷售額的影響有顯著不同,而不同廣告時段對廣告銷售額則無顯著影響。
(2)事後檢定(Post hoc):
事後檢定目的為檢定當多組樣本平均數有顯著差異時,詳細的顯著差異是發生在哪幾組之間。
關於事後檢定有許多種檢定方式,本次以Tukey及Bonferroni法為例,兩種方法的結果皆顯示廣告方式A與B這組及廣告方式A與C這組之間有顯著差異。
SPSS範例檔可從下列連結抓取,僅供同學練習使用:
五、R語言教學範例 code Example:
我們上面介紹過SPSS的操作方式,以下用R語言分析二因子變異數分析的交互作用。
## Default
aov(response ~ factor, data=data_name)
TukeyHSD(result,conf.level=0.95)
【例題】分析棒球投手在早場或晚場的球賽中穿著自己習慣的球鞋與自己不習慣的球鞋時,在投球表現上是否有差異?
本題的例子為兩個觀察因子(球賽時間、穿著球鞋),故選擇Two-Way ANOVA檢測樣本的平均值是否不同
(一)試問球賽時間是否影響投球表現?
虛無假說(Null hypothesis)→球賽時間不會影響投球表現
對立假說(alternative hypothesis)→球賽時間會影響投球表現
(二)試問穿著慣用球鞋是否影響投球表現?
虛無假說(Null hypothesis)→慣用球鞋不會影響投球表現
對立假說(alternative hypothesis)→慣用球鞋會影響投球表現
(三)輸入棒球投手分別在個情況下投球表現資料
baskball <- read.table(“E:/baskball.txt”,header=TRUE)
tapply(Made,Time,mean)
Morning Night
30.500 31.875
tapply(Made,Shoes,mean)
Favorite Others
32.750 29.625
→描述性統計呈現,晚場投球表現比早場表現好;穿著慣用球鞋表現比非慣用時好
(四)使用Two-Way ANOVA檢驗交互作用
int <- aov(Made ~ Time*Shoes)
summary(int)
Df Sum Sq Mean Sq F value Pr(>F)
Time 1 7.562 7.562 0.3441 0.5684
Shoes 1 39.062 39.062 1.7773 0.2072
Time:Shoes 1 18.062 18.062 0.8218 0.3825
Residuals 12 263.750 21.979
→結果發現,球賽時間與是否穿著慣用球鞋的交互作用項(Interaction)之F統計值為0.8218,顯著性p值=0.3825>0.05,無法拒絕虛無假說。
→球賽時間與是否穿著慣用球鞋對於投球表現上並無顯著交互作用。由於交互作用不顯著,本研究進一步探討主要效果。
(五)使用Two-Way ANOVA檢驗主效果(移除交互作用項)
noint <- aov(Made~Time + Shoes)
summary(noint)
Df Sum Sq Mean Sq F value Pr(>F)
Time 1 7.562 7.562 0.3489 0.5649
Shoes 1 39.062 39.062 1.8020 0.2024
Residuals 13 281.812 21.678
→結果發現,球賽時間對於投球表現的影響,F統計值為0.3489,顯著性p值=0.5649>0.05,無法拒絕虛無假說。
→球賽時間對於投球表現上並無顯著影響。
→穿著慣用球鞋對於投球表現的影響,F統計值為1.8020,顯著性p值=0.2024>0.05,無法拒絕虛無假說。
→是否穿著慣用球鞋對於投球表現上並無顯著影響。
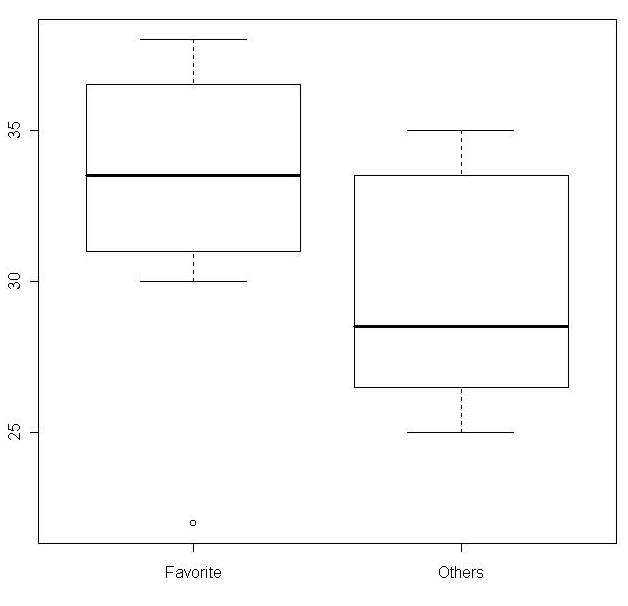
根據Boxplot繪圖可知兩組主效果的差異不大。
boxplot(Made ~ Time)
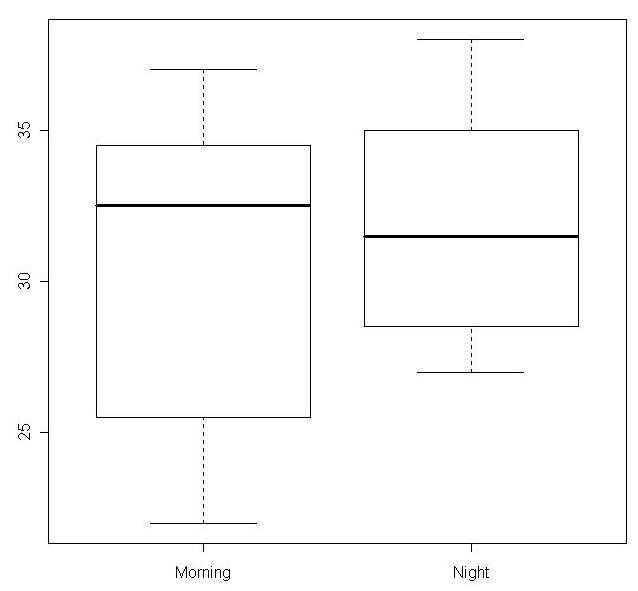
boxplot(Made ~ Shoes)
感謝大家收看本次教學~


封面圖-500x383.png)


