卡方檢定用於分析兩類別變數間的關係,本次介紹的內容為獨立性檢定,以下將詳細說明原理及SPSS操作。
一、使用狀況:
卡方獨立性檢定適用於分析兩組類別變數的關聯性。
同一樣本中,兩個變項的關聯性檢定,也就是探討兩個類別變項(例如:性別和結婚狀態)之間,是否為相互獨立,或者是有相依的關係存在,若是達到顯著,則需進ㄧ步查看兩個變項的關連性強度。
二、前提假設:
(一)所有的變項為類別變項(categorical variable)
(二)樣本須為獨立變項(Independent variable)→第一組的樣本不影響第二組的樣本;第二組的樣本也不影響第一組。
(三)每一檢定細格(cell)內的數據應該設為頻率或計數數目,而不是百分比或是經過轉換之數據。
(四)至少有80%以上的細格,其樣本數大於5,亦即樣本數目至少要為細格數目的五倍。
三、假說檢定(Hypothesis Testing):
| Disease(b) | ||||
| Exposure(a) | yes | no | total | |
| yes | A | B | A+B | |
| no | C | D | C+D | |
| total | A+C | B+D | A+B+C+D | |
(一)卡方值之計算公式如下:

χ2為每一細格之卡方數,O為觀察次數,E為期望次數,期望次數的計算是以每行與每列之交乘值除以總數(Total)便得到期望值,例如:[(A+B)*(A+C)]/Total為A Cell之期望值。
此公式表示自i細格至j細格中,觀察值與期望之差異之總和,若差異越大則表示兩變數之間越有關聯性,越容易顯著。
其假說檢定如下:
H0: χ2為0
H1: χ2不為0
自由度=(a-1)* (b-1), a與b為行列分組數目。
四、SPSS 操作Example:
(一)在SPSS中輸入欲分析之資料。
本次分析想要來了解,上班族失眠症狀跟感到疲勞是否有相關性,兩個變項之間是否相互獨立,這筆資料共有61筆數據。
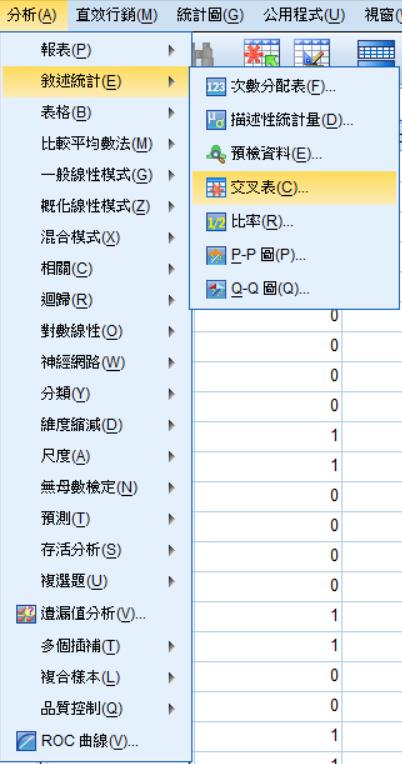
(二)卡方獨立性檢定:分析→敘述計→交叉表
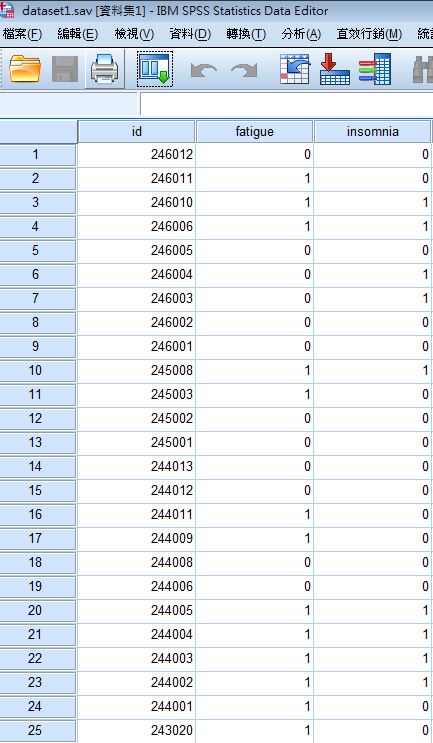
(三)以自變項為列,依變項為欄(直行)→統計量選擇「卡方分配」
自變項:fatigue疲勞(是否感到疲勞,為類別變項,0代表沒有感到疲勞1代表感到疲勞)
依變項:insomnia失眠(是否有在失眠的症狀,為類別變項,0代表沒有症狀1代表有症狀)
統計量選項:卡方分配
(四)檢定結果:
(1)基本描述性統計:
61位受試者包含在本次分析中,不感到疲勞的人為23人,感到疲勞的有38人;
無失眠症的有42人,有失眠症的有19人。其中,不感到疲勞的23人中有2人有失眠症,而感到疲勞的38人中有17人有失眠症,接著進一步看以下的卡方檢定檢驗這兩種比例的關聯性。
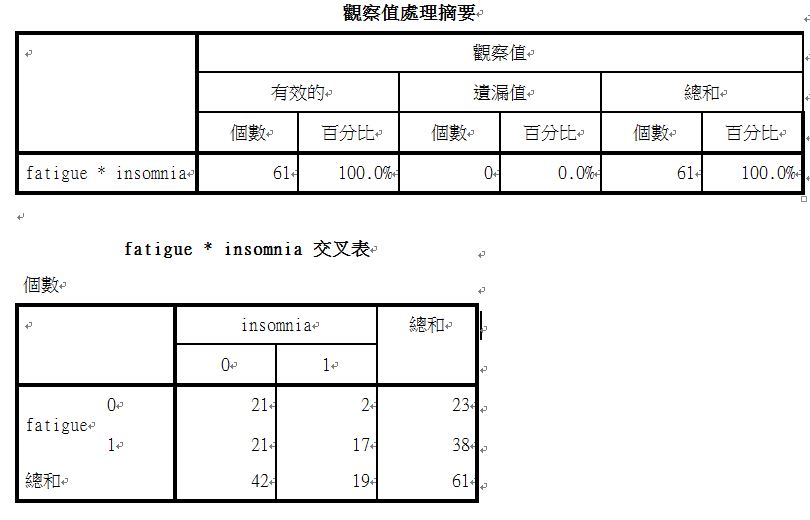
(2) 卡方獨立性檢定:
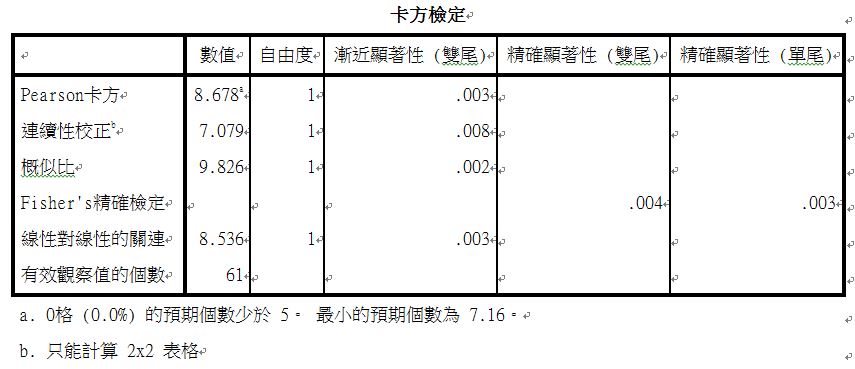
Pearson卡方值小於0.05時,表示有統計上顯著差異,本次結果可以得知:0.003小於0.05,感到疲勞在是否有失眠症狀上,達顯著差異,表示疲勞與失眠症之間有顯著關係。
補充:在卡方檢定中,一般要求期望次數不得小於1, 並且不得有20%以上細格的的期望次數小於5→不然則建議合併相鄰的行或列,或採用Yate’s correct test,或採用Fisher’s Exact Test
以上教學分析檔可從下列網址下載,僅供同學練習使用。



封面圖-500x383.png)

