存活分析用於探討醫學中病人的死亡及存活機率,用以判斷醫療(藥)介入效果,以下將詳細說明。
一、使用狀況
存活分析,在生醫領域常常被使用,特別是在於想要了解特定某疾病的人口死亡率跟存活率時,我們會使用存活分析。另外一方面,在藥物治療上,兩個藥對於疾病的治癒療效如何,也可以透過存活分析來區辨。舉例來說:新藥與舊藥的比較,新藥是否會減少疾病的死亡率且增加存活率,可以透過比較了解新藥療效,再透過這樣的臨床試驗後,確定新藥成效便進一步發售於市面。
二、理論說明
存活分析是指在某特定時間起經過一段時間的觀察追蹤,直到特定事件(event)的發生。在生醫領域上,起始時間(starting event time point, zero time point)通常是確立疾病時間或是手術的時間點。而我們稱中間這段時間的觀察追蹤為follow-up。而特定事件的發生在生醫上會是死亡或是疾病復發(endpoint or event)。舉例來說:今天我們想了解胰臟癌的存活時間,起始點就會是在門診的時候被確定得到胰臟癌開始,接著一段時間的觀察追蹤,確認個案死亡就停止追蹤。第二個例子:像是大腸直腸切除手術為起始點,而復發入院為終止的時間點,追蹤手術預後的成效如何。
然後,在完美的情況之下,我們可以得到個案從起始時間觀察追蹤到事件發生。但是實際情況,有可能發生追蹤到一半,個案就消失了(例如:換了電話或是沒有回醫院複診),這樣的情況我們就稱為設限(censoring)。如果說是跟疾病沒有相關的事件發生呢?我們又該如何處理。在大腸直腸切除手術的例子中,如果個案車禍意外過世了,那我們也稱這樣的情況是我們沒有興趣的事件(Event of interest)為設限(censor),同時我們也稱之為競爭死因。
什麼時候個案會變成設限呢?
- 研究結束的時候,個案並沒有死亡(event)
- 個案在研究過程中失聯了
- 個案在研究過程中被剔除(原因可能是競爭死因或是不良藥物反應)
三、案例說明
讓我們來舉個例子:
今天有A到F六位病人得到胰臟癌,我們從研究開始點追蹤至研究結束。A:在研究結束的時候,還沒有死亡,但之後過世了;B跟E: 在研究結束前失去聯絡;C: 在研究結束的時候,因為其他原因過世;D: 在研究開始前就被診斷成胰臟癌,但研究開始的時候並沒有死亡,追蹤一段時間死亡;F: 在研究開始前就被診斷成胰臟癌,研究結束的時候,還沒有死亡,但之後過世了。
我們可以將以上資訊畫成圖,其中死亡的以叉叉表示,設限以圓缺表示,如下所示。
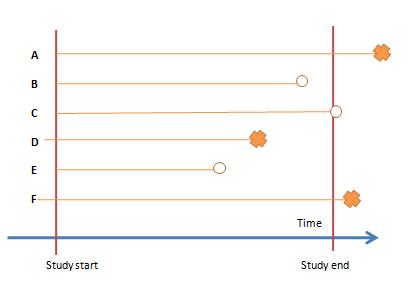
由下表可以發現A跟F雖然已經死亡,但在研究結束的時間點並沒有死亡,所以符合設限的第一個情況:研究結束的時候,個案並沒有死亡。而在研究過程中只有D符合我們的事件定義。可以看出來其實事件(event)跟設限(censor)兩者可以合成單一變項,我們用狀態status表示。有人會有疑問說B跟E同樣是設限,他們可以代表什麼樣的涵義呢?回到存活分析的定義,我們可以獲得的是到事件發生前的時間長短,也就是存活的長度,雖然我們不知道失聯後發生什麼事,但我們可以確定在這之前他們並沒有死亡,因此可以提供存活時間的長短。
| ID | Event (1=event) | Censor (1=censor) | Status (1=event; 0=censor) |
| A | 0 | 1 | 0 |
| B | 0 | 1 | 0 |
| C | 0 | 1 | 0 |
| D | 1 | 0 | 1 |
| E | 0 | 1 | 0 |
| F | 0 | 1 | 0 |
將存活時間納入,我們可以整理成下列表格
| ID | Survival time(months) | Status (1=event; 0=censor) |
| A | 12 | 0 |
| B | 8 | 0 |
| C | 12 | 0 |
| D | 7 | 1 |
| E | 5 | 0 |
| F | 12 | 0 |
在依照時間軸排序的話,在研究開始五個月後,E失聯了,所以剩下個案數為5。在七個月的時候,D死亡,剩下個案數為4。以此類推,可以得出在某時間點下,存在個案數為多少。
| ID | Survival time(months) | Status (1=event; 0=censor) | Number left |
| E | 5 | 0 | 5 |
| D | 7 | 1 | 4 |
| B | 8 | 0 | 3 |
| A | 12 | 0 | 3 |
| C | 12 | 0 | 3 |
| F | 12 | 0 | 3 |
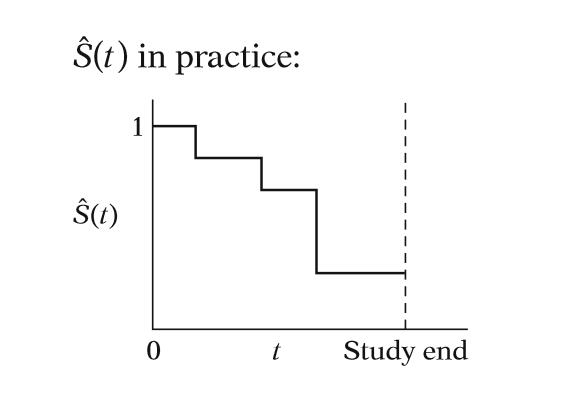
之後再透過存活函數,可以畫出下列隨著時間變化的存活分析圖。
四、存活函數 (Survival Function)介紹
存活函數呈現的是在某特定時間點之下,個案可以活過特定時間點的機率是多少,是一個遞減的函數(Decreasing function)。
𝑆( 𝑡) = 𝑃 (𝑇 > 𝑡)
t 是時間點
𝑆( 0 )= 1
𝑆 (∞) = 0
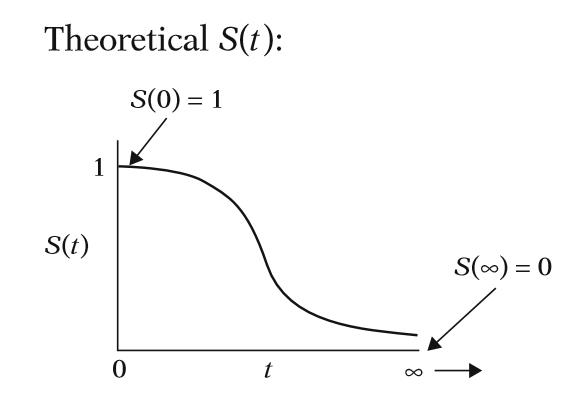
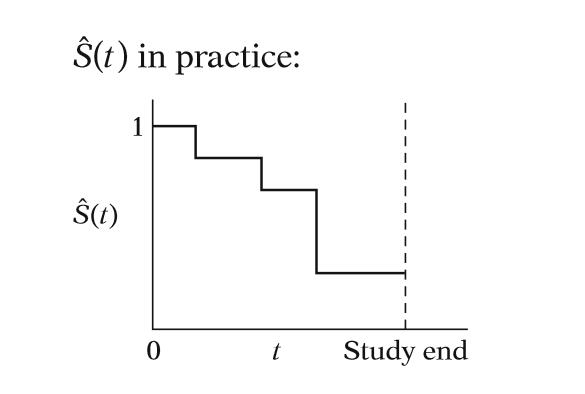
理想(左圖)與現實情況(右圖)的函數圖形如下
在實際情況可以看到每個時間點如果像階梯往下的部分,代表的是有個案的死亡,下降的幅度越大代表死亡個數越多。
在無母數的假定之下,存活函數的估算可以分成Life-table method跟Kaplan-Meier method。我們這次先分享Life-table method的使用方法。
五、SPSS 操作Example
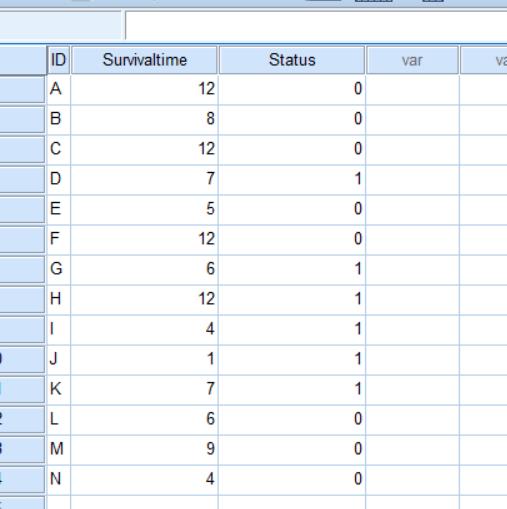
1、在SPSS中輸入欲分析之資料。
目前有14位胰臟癌的病人,我們追蹤了12個月,獲得他們到過世前存活時間的資料,我們利用這筆資料,分析胰臟癌的存活率。
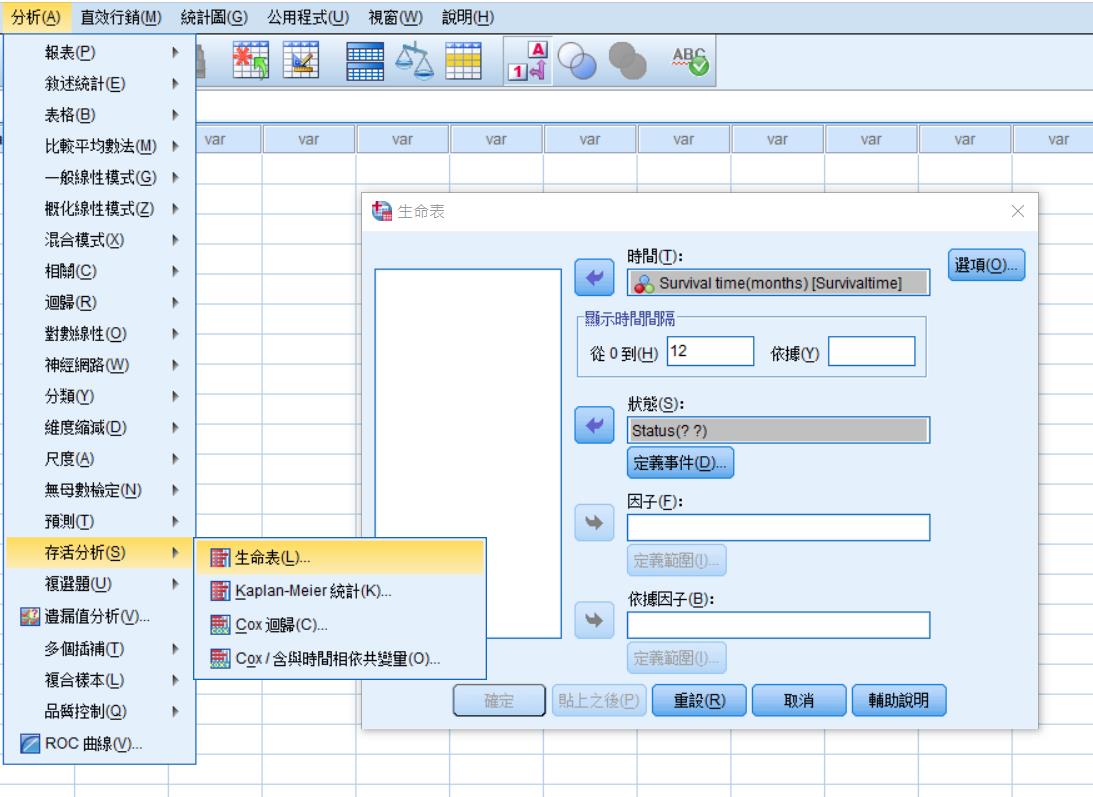
2、分析→存活分析→生命表
3、在生命表內
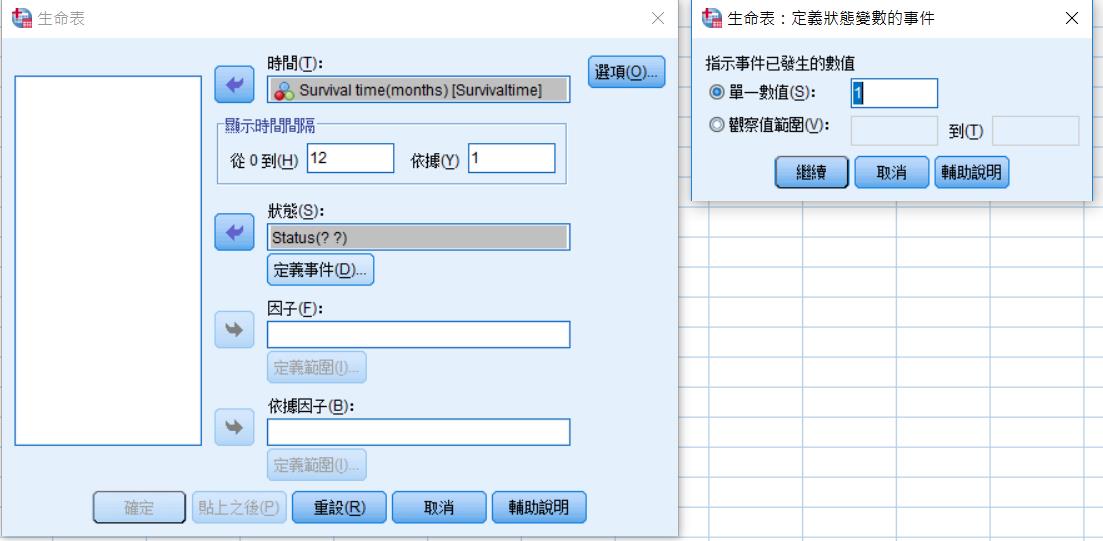
時間:點選Survival time,時間間格從0到12,因為追蹤時間是12個月就填12,依據的則填1。
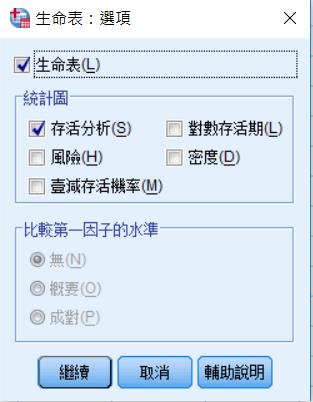
狀態:選event的變項,定義事件要定義什麼樣的值為event,所以填1。本次並沒有多組比較,所以因子就先不管。另外在右上角的選項裡面,勾選生命表跟存活分析
4、結果:
在生命表上可以看到表格依照時間順序排列,而進入區間的個數隨著時間遞減。在累積比例的變項,我們可以看到在超過特定時間點的存活機率。舉例來說:想要知道罹癌之後活超過七個月的存活率為0.57。
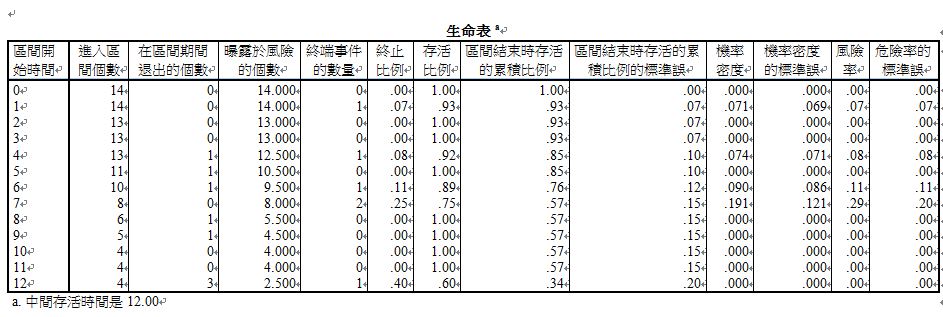
而圖的部分則是可以看特定月份存活率的大幅下降,第八個月的時候,存活率大幅下降降到0.57左右。
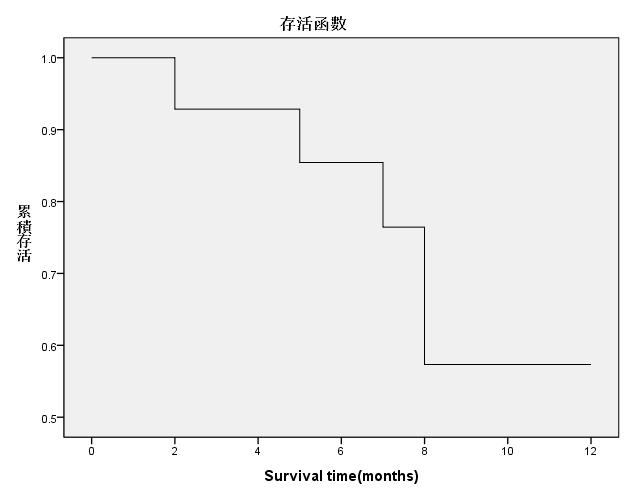
本次範例操作檔案可自下列網址下載,僅供教學使用。



封面圖-500x383.png)

