算術平均數(arithmetic mean)是一般常見的集中趨勢量數之一,本篇文章將透過(1)定義、(2)公式、(3)特性以及(4)SPSS算術平均數分析範例,讓大家能更瞭解算術平均數。
一、定義
算術平均數為資料數值總和除以資料個數。
二、公式
介紹公式之前,我們要先確認資料是否有進行分組。
無分組的資料範例如下:
3, 6, 7, 25, 31, 33, 38, 42, 46
在無分組的資料範例中,我們知道每一個資料的數值,因此根據算術平均數的定義,我們可以列出以下公式:
若資料為母體,則公式為:
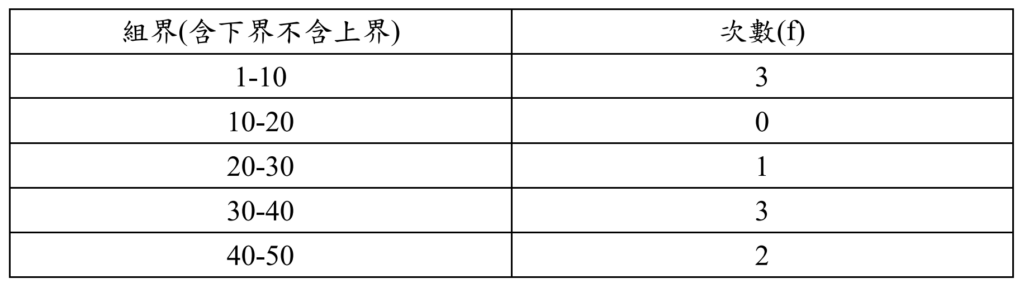
有分組的資料範例如下:
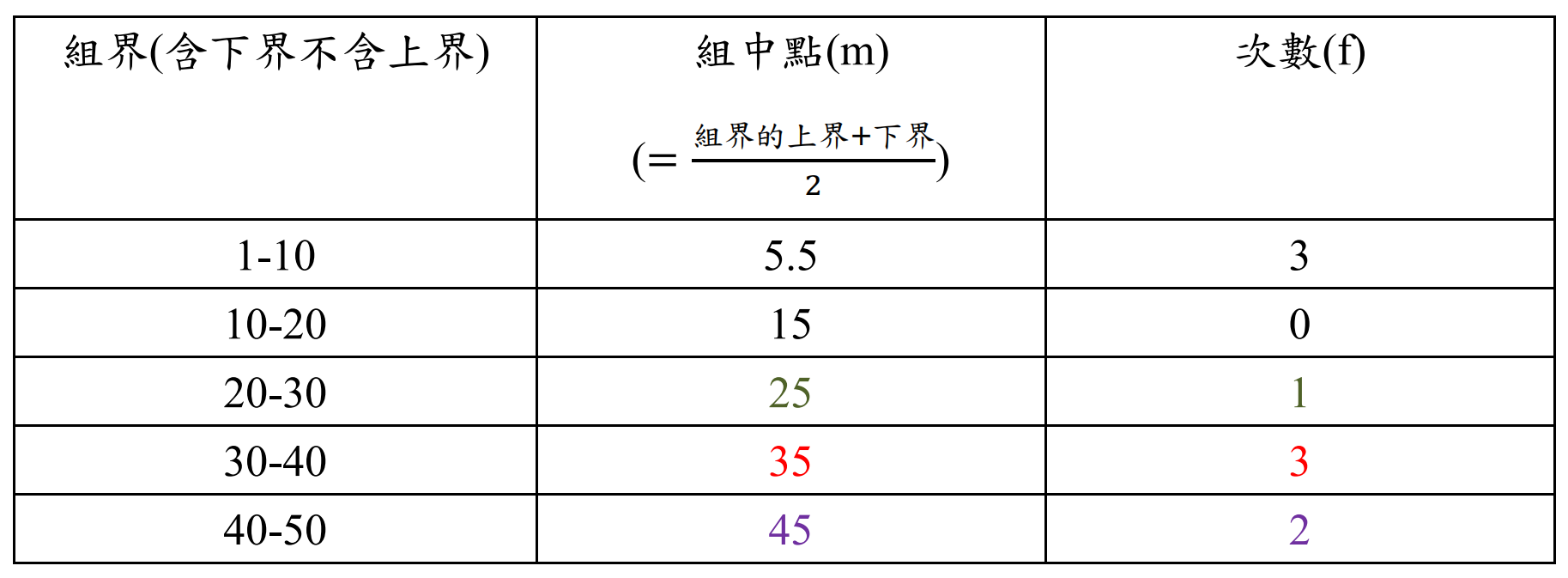
在有分組的資料範例中,我們知道的是『組數(k)』、『組界』以及『次數(f)』,因此我們先取每一組的組中點(m)作為該組的代表數值。
接著,我們就可以透過組中點及次數將分組資料轉成以下未分組資料:
5.5, 5.5, 5.5, 25, 35, 35, 35, 45, 45
由於每一組的總和會等於『組中點(m)』x『次數(f)』,故我們可以將算術平均數的原始公式改寫為:
三、算術平均數特性
(一)、每一個資料數值皆增加Y,則新的算術平均數為原始算術平均數增加Y
(二)、每一個資料數值皆乘上Z,則新的算術平均數為原始算術平均數乘上Z
(三)、每一個資料數值與算術平均數相減的數值,加總為零。
(四)、每一個資料數值與算術平均數相減的數值平方,加總為最小值。(與其他任意數值(R)相比)
(五)、容易受到極端值的影響
四、SPSS算術平均數分析範例
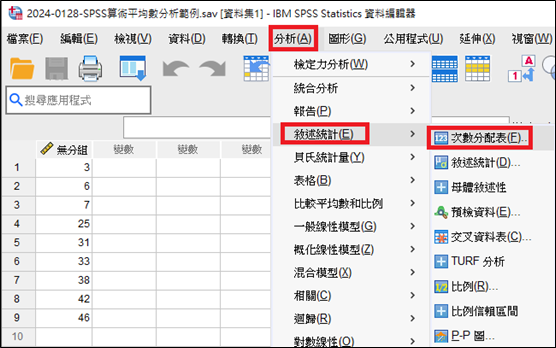
本次範例以上述的無分組資料作為範例資料。首先,我們點選【分析(A)】→【敘述統計(E)】→【次數分配表(F)】。
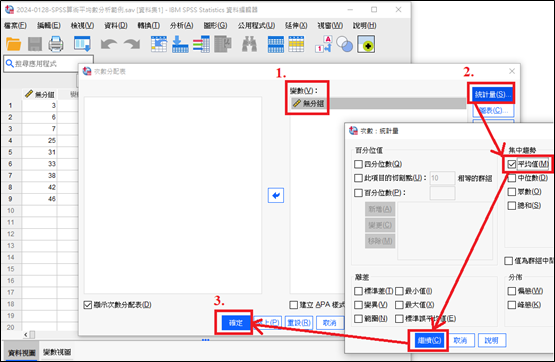
接著,將無分組選入右方的變數欄位,然後點選【統計量(S)】,在統計量視窗右邊的『集中趨勢』部分,勾選『平均值(M)』,按下【繼續(C)】,再按下【確定】。
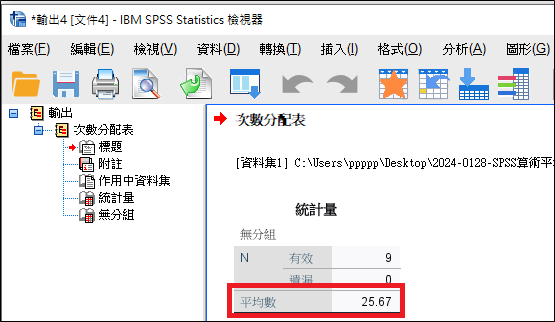
從分析結果中,即可得到無分組的算術平均數為25.67。
以上就是本次文章的介紹內容,希望對於大家有所幫助,之後也會再介紹其他常見的集中趨勢量數給大家,方便的話再請幫我們留個好評,謝謝。


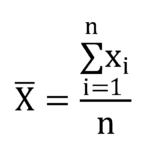
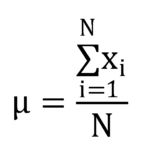
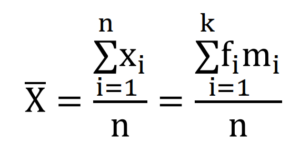
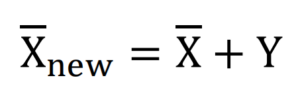
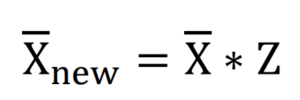
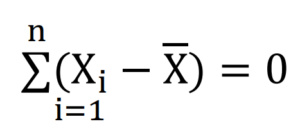
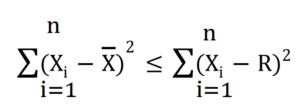

封面圖-500x383.png)

