曼惠特尼U檢定(Mann-Whitney U test)是用於比較兩組獨立樣本間中位數是否有差異的檢定,是當獨立樣本t檢定違反基本假設時所使用的檢定方式(例如:常態分配、變異數同質性假設等等)。
由於Mann-Whitney U test是無母數的統計方式,其適用於以下三種情形:
1、非常態資料
2、小樣本資料(N<30)
3、依變數可以為次序型資料
以下將逐步介紹Mann-Whitney U test的數學公式,以及SPSS的統計操作過程。
一、假設檢定
Mann-Whitney U test的假設檢定一般會寫成以下形式。
H0:兩組樣本的母群體相同 (Two populations are equal)
H1:兩組樣本來自不同母群體
也有部分研究者會用比較兩組的中位數的方式來設定Mann-Whitney U test虛無假設(Null hypothesis) (H0:Median1= Median 2),類似我們獨立樣本t檢定的作法(H0:u1=u2)。
二、統計公式
Mann-Whitney U test的統計過程及公式可以參考以下步驟,我們拿一筆資料當作範例進行說明。這筆範例資料中,實驗組與控制組各有三筆分數,我們進行以下五個步驟。
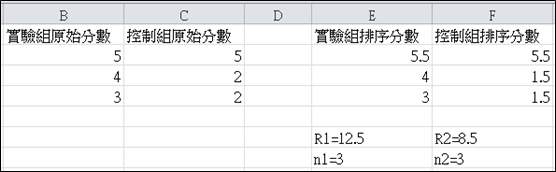
(一)、將兩組人的分數一起進行排序,兩組樣本數分別為n1及n2
在這六筆資料中,分數原始數據排序依序為2、2、3、4、5、5,n1及n2皆為3。
(二)、將所有分數從最低(設為rank 1)排至最大(設為rank N),若有重複的原始分數則取其Rank的平均,接著進行兩組別的Rank加總
由於第一步驟最前面兩筆及最後兩筆數字一樣,因此我們在排序上取平均,最終的Rank值為1.5、1.5、3、4、5.5、5.5,我們可以將其排序整理成以下表格。
| 原始分數 | 2 | 2 | 3 | 4 | 5 | 5 |
| 初始排序 | 1 | 2 | 3 | 4 | 5 | 6 |
| 調整後 | 1.5 | 1.5 | 3 | 4 | 5.5 | 5.5 |
根據上述表格,我們可以算出R1為12.5,R2為8.5,接著進行第三步。
(三)、計算出U1及U2值
U1 & U2之公式如下圖。
根據公式我們可以得知
(四)、取U=Min(U1 ,U2)
從6.5及2.5的最小值,故U為2.5。
(五)、進算出Z值並進行檢定
Z值公式如下圖,由下圖公式計算可知,Z值為-0.872未達顯著,表示兩組之間差異不大。
三、SPSS操作教學
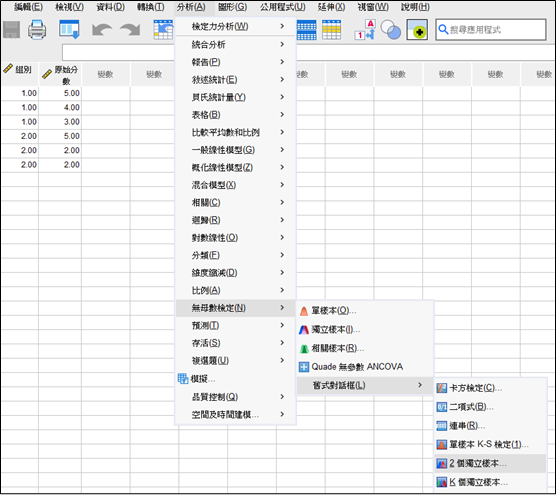
(一)分析路徑
打開SPSS資料檔,分析->無母數檢定->舊式對話窗->2個獨立樣本
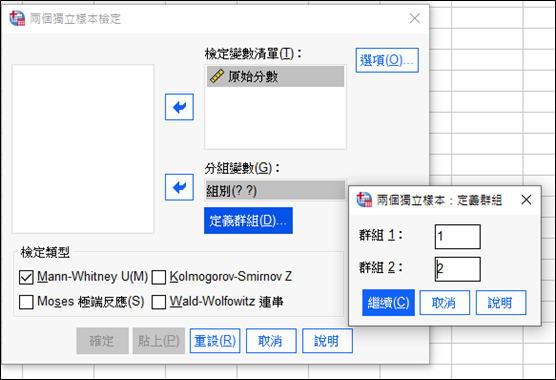
(二)選取變數
將組別設定為1、2,檢定變數放入原始分數,勾選Mann-Whitney U test即可按確定。
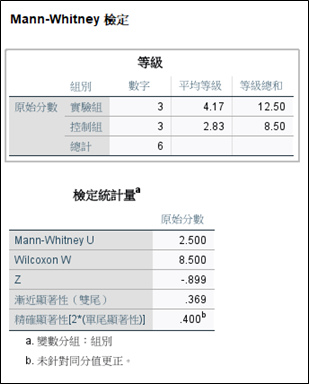
(三)分析結果
由結果可知,統計檢定Z值為-0.899,未達顯著,表示兩組之間無顯著差異。
此外,由SPSS結果我們可以發現,其計算公式跟上述公式算出來的結果略有差異,我們透過公式算出來的數據為-0.872,SPSS計算出來的為-0.899。這個部分SPSS應該是採用了以下的調整公式,為了解決資料中有相同評分時須調整標準差的問題。
在下述的公式中,g為有相同評分的組數,t為同分組數內的數值個數。舉例而言,本範例中有相同評分的有2組(2 & 5),因此g為2;而這2組中各有兩個數字(2、2 & 5、5),因此t為2。
以上為本次Mann-Whitney U test的說明詳解,若您喜歡的話再幫我們留個好評,謝謝您的觀看,我們下次見。


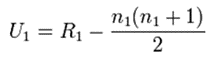
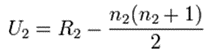

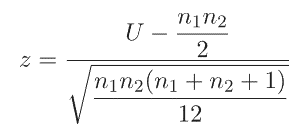
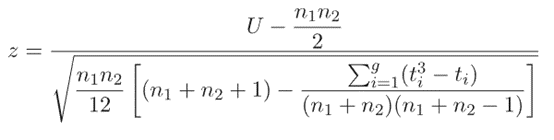

封面圖-500x383.png)

