對於變異數分析,大家最常聽到的統計方法是one-way ANOVA,指的是單因子單變量變異數分析,也就是只有一個依變數(Y),用來分析自變數對依變數各組平均數的差異。
有關ANOVA的介紹與SPSS操作,大家可以參考網站中的這篇文章。
至於one-way MANOVA,則指單因子多變量變異數分析,也就是同時有兩個以上的依變數(Y),可以同時檢驗多個依變數各組平均數的差異。
這時有人便有疑問,有多個依變數,為什麼不進行多次的ANOVA檢定就好?
其實,MANOVA除了能更快速得出結果之外,也可以降低出現型Ⅰ錯誤的機會,還能觀察自變數在多個依變數之間的總體差異。
註:有關型Ⅰ錯誤之說明,可以參考網站中的這篇文章。
說了那麼多,大家是否還是有些困惑呢?以下便舉一個例子來看看:
使用範例
若以大學跨系所某學程的期末總成績為例,「總成績」為依變數,假設期末總成績包含了「經濟學」、「會計學」、「統計學」三種不同的成績,此時依變數便有三個,便需要進行one-way MANOVA分析。
當我們想要知道「總成績」是否會因為學生科系類別(文組、理組、醫學類組)不同而有所差異?
此時學生科系類別便是因子,不同科系類別學生的期末成績為各自獨立的樣本,但總成績又包含經濟學、會計學、統計學三種成績,所以要比較總成績高低的差異,便可以將三種成績同時當作依變數,同時一起進行變異數分析,這時的分析方法便是「獨立樣本單因子多變量變異數分析」。
SPSS操作
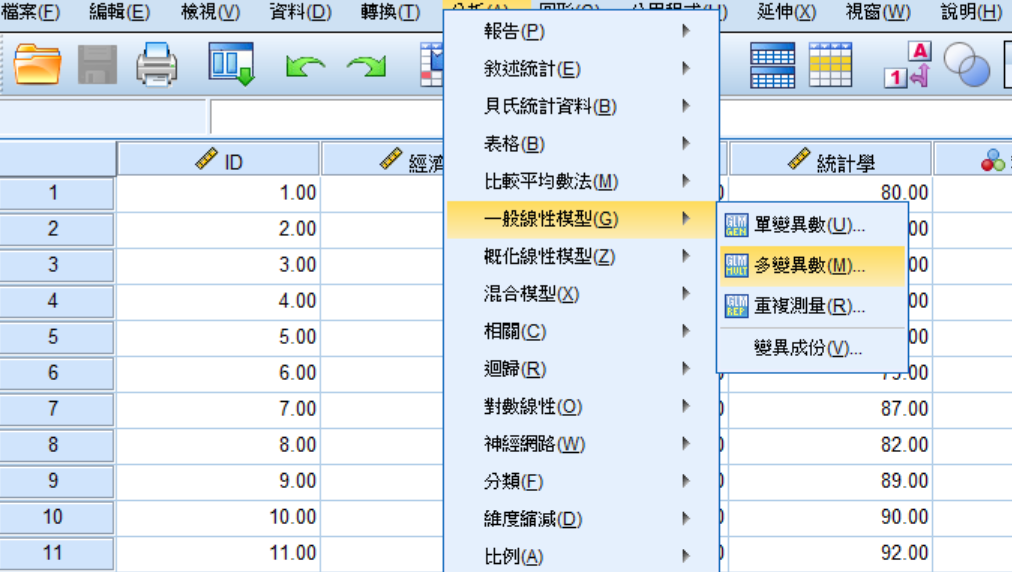
Step 1:點選「分析→一般線性模型→多變異數」
Step 2:將「經濟學」、「會計學」、「統計學」放入應變數,「科系類別」放入固定因子,並點選「選項」
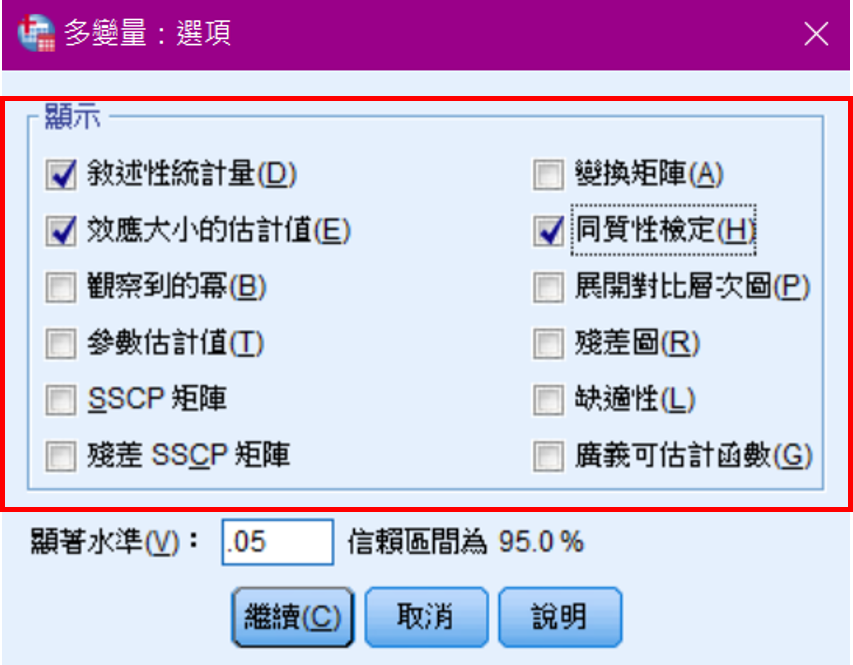
Step 3:勾選「敘述性統計量」、「效應大小的估計值」、「同質性檢定」
Step 4:報表解讀
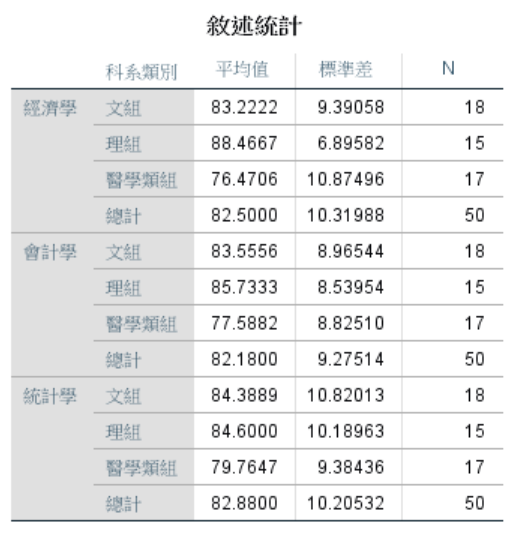
由上圖可發現,理組在「經濟學」、「會計學」、「統計學」的平均成績高於文組和醫學類組。
但這個結果是否具有統計學上的差異呢?仍需要進一步的檢定。
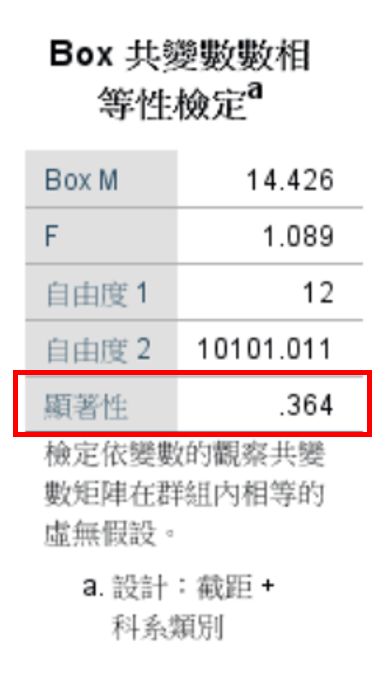
在Box檢定中,若P>0.05則滿足協方差(兩個變數的整體誤差)同質性的要求,這也是one-way MANOVA的適用條件。
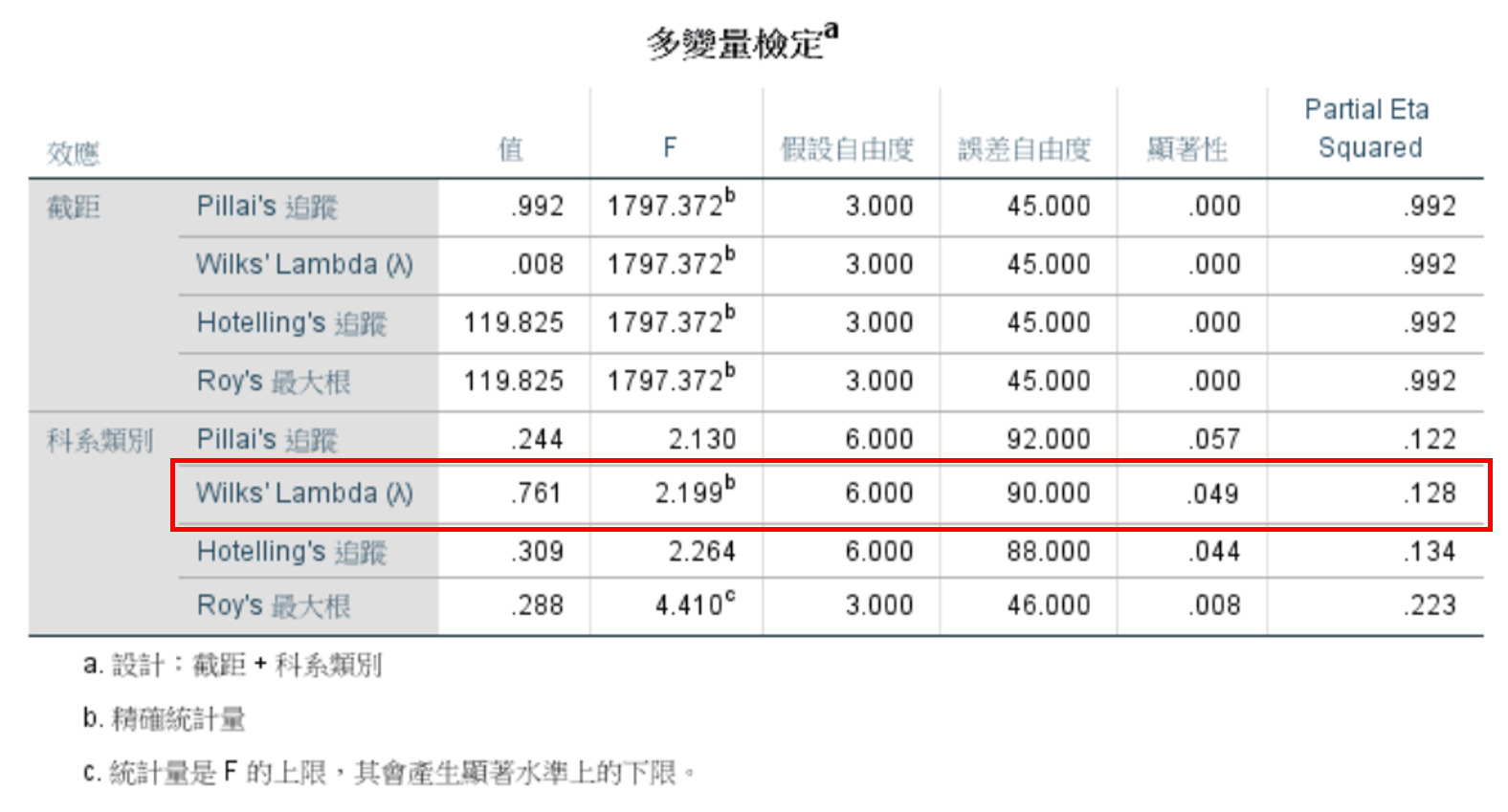
在多變量檢定中,可發現Wilks’ Lambda的P<0.05,也就是學生科系類別對於總成績在統計上有顯著差異。
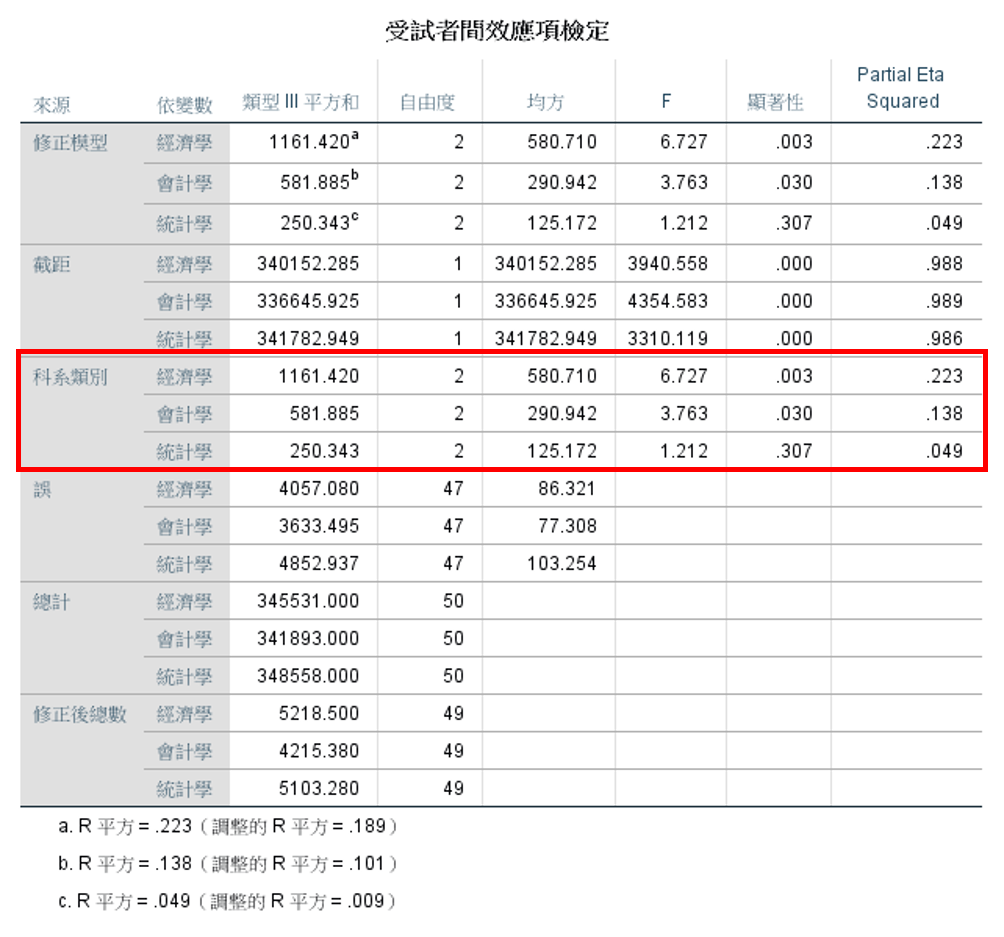
再來觀察不同變數的差異情形,上圖顯示在總成績中,學生科系類別對經濟學(P<0.05)與會計學(P<0.05)有顯著差異,而對於統計學(P>0.05)則並無顯著差異。
以上便是one-way MANOVA的用法,你學會了嗎?




封面圖-500x383.png)

