當依變數是類別變數時,使用羅吉迴歸進行分析;而類別變數可分為二分類、多分類和有序分類。
本篇文章介紹有序羅吉斯迴歸分析- R語言的操作,細節如下所述。
#補充:羅吉斯迴歸分析可分為以下幾個主要方面:
- 二元羅吉斯迴歸(Binary Logistic Regression):
用於處理目標變數是二元的情況,即只有兩個可能的結果。例如:預測學生是否通過考試(通過/不通過)。
- 多元羅吉斯迴歸(Multinomial Logistic Regression):
適用於多類別目標變數的情況,其中目標變數有三個或更多的類別。例如:預測學生在一個班級中的成績等級(優/良/差)。
- 有序羅吉斯迴歸(Ordinal Logistic Regression):
用於處理有序類別的目標變數,這些類別之間有固定的順序。例如:預測客戶滿意度的高、中、低。
一、分析目的
當依變數為有序類別變數(也就是能分出大小、有序等級,但差距不一定相同)時,例如所得收入的程度(低/中/高),可以採用有序羅吉斯迴歸進行分析。
二、適用條件
使用有序羅吉斯迴歸分析需要滿足以下5個條件:
條件1:依變數為有序類別變數。
條件2:自變數的類型為類別型變數與連續型變數。
條件3:變數為獨立性(資料值彼此不相關)。
條件4:滿足平行性檢驗(即比例優勢假設)。
條件5:自變數之間無多重共線性。
#補充:比例優勢假設
意思是無論依變數的分割點在什麼位置,模型中各個自變數對依變數的影響不變,也就是自變數對依變數的迴歸係數與分割點無關。
三、R語言操作範例
(一)範例介紹
某研究生想瞭解「性別」、「年齡」和「收入」與「教育程度」之間的關係。
(二)資料匯入
Testdata<-read.csv(“456.csv”,header=T) #將資料匯入到指定的變數,也就是Testdata
View(Testdata) #瀏覽資料內容
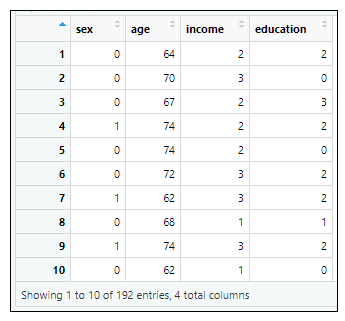
→根據執行結果:在資料集中共有4個變數和192個觀察資料,4個變數分別為:
性別(sex;0:女性、1:男性)、年齡(age)、收入(income;1:低、2:中、3:高)、
教育程度(education;0:國中以下、1:高中職、2:大學、3:研究所)。
##重新定義分組變數##
#將變數「sex」、「income」、「education」設置為因子(factor)變數並為各類別水準 (levels)給予指定名稱。
Testdata$sex <- factor(Testdata$sex,levels = c(1,0),labels = c(“man”,”woman”))
Testdata$income <- factor(Testdata$income,levels = c(1,2,3),labels = c(“low”,”medium”,”high”))
Testdata$education <- factor(Testdata$education,levels = c(0,1,2,3),labels = c(“Secondary”,”Vocational”,”University”,”Institute”))
str(Testdata) #查看數據結構
##定義參照組##
Testdata$Income <-relevel(Testdata$Income,ref=”low”) #為Income設置參照組為” low “
#補充:參照組(reference group)
- 一個具有K個水準的類別變項,可以轉換成K個虛擬變項,然在實際執行迴歸分析時,第K組是K-1組的數值全部為0,故實際只要K-1組,以免造成變項的多元共線性問題。
- 未經虛擬處理的水準,即稱為參照組。
- 參照組不一定是最後一個水準,而宜取用內容明確清楚,樣本數適中的水準作為參照組。如「其他」就不適合做為參照組;有順序關係時,如教育水準,可以選擇最高等級、最低或中間等級,作為參照組。
(三)適用條件判定
- 條件1判斷(依變數判斷)
本範例的依變數為教育程度,且為有序類別變數。
滿足適用條件1「依變數為有序類別變數」。
- 條件2判斷(自變數判斷)
本範例有三個自變數,性別和收入為類別變數,年齡為連續變數。
滿足適用條件2「自變數的類型為類別型變數與連續型變數」。
- 條件3判斷(獨立性判斷)
本範例各研究物件的觀測值都是獨立的,不存在互相干擾的情況。
滿足適用條件3「變數為獨立性」。
- 條件4判斷(平行性檢驗)
##平行性檢驗##
用於檢驗自變數偏回歸係數是否保持一致。
平行性檢驗的原假設為模型滿足平行性,因而如果P值大於0.05則說明模型接受原假設,即符合平行性檢驗。反之如果P值小於0.05則說明模型拒絕原假設,模型不滿足平行性檢驗。平行性是有序羅吉斯迴歸的前提條件,如果不滿足平行性,建議使用多元羅吉斯迴歸模型。
install.packages(“VGAM”) #安裝套件:VGAM
library(VGAM) #載入套件:VGAM
#建立模型
#按照符合平行性進行擬合(parallel = TRUE, 指模型滿足平行性假設)
vglmH0<-vglm(ordered(education) ~ sex+income+age, data=Testdata, family=cumulative(parallel = TRUE))
#按照不符合平行性進行擬合(parallel = FALSE, 指模型不滿足平行性假設)
vglmH1<-vglm(ordered(education) ~ sex+income+age, data=Testdata, family=cumulative(parallel = FALSE))
#建立假設
#H0:平行性模型與非平行性模型擬合效果一致 = vglmH0
#H1:平行性模型與非平行性模型擬合效果不一致 = vglmH1
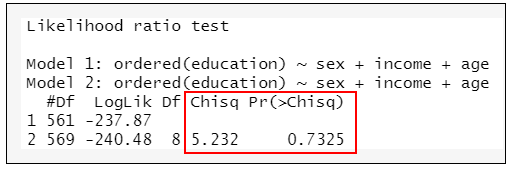
lrtest(vglmH1,vglmH0) #計算兩種模型擬合結果是否一致
→根據執行結果:顯示X2=5.232,P=0.7325>0.05接受原假設,表示Model1(vglmH0)成立,滿足適用條件4「滿足平行性檢驗」。
(四)變數篩選
install.packages(“MASS”) #安裝套件:MASS
library(MASS) #載入套件:MASS
##單因素迴歸分析##
fit1<-polr(education~sex,data=Testdata)
fit2<-polr(education~age,data=Testdata)
fit3<-polr(education~income,data=Testdata)
##似然比檢驗##
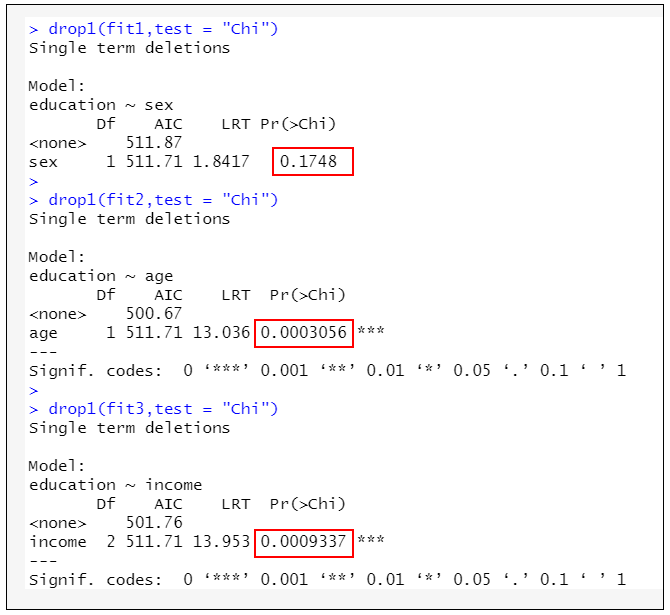
drop1(fit1,test = “Chi”)
drop1(fit2,test = “Chi”)
drop1(fit3,test = “Chi”)
→根據執行結果:顯示在單因素分析中「年齡」和「經濟水準」與依變數的關聯是有顯著的差異(P<0.05),「性別」與依變數的關聯是無顯著的差異(P=0.1748)。
##計算係數的可信區間##
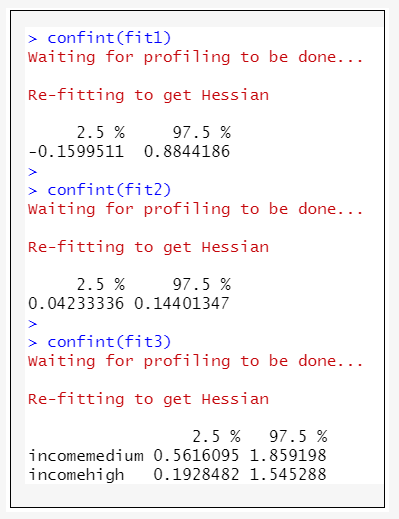
confint(fit1)
confint(fit2)
confint(fit3)
→根據執行結果:得到每個單因素模型中變數係數的95%CI,若信賴區間包含0,則說明該變數在模型中無顯著的差異;結果顯示「性別」的95%CI包含0。而「經濟水準」和「年齡」的95%CI未包含0。因此,多因素迴歸模型中可納入「年齡」、「經濟水準」兩個變數。
經過剛剛的變數篩選,找到無顯著差異的變數「性別」進行移除,再建立最終的迴歸模型。
##建立新的迴歸模型##
fit<-polr(education~age+income, data=Testdata)
(五)適用條件判斷(續)
- 條件5判斷(多重共線性診斷)
##共線性診斷##
變異數膨脹因數(Variance Inflation Factor,VIF):
為預防迴歸模型存在共線性問題,可以使用VIF來判斷解釋變數間是否存在高度多重共線性。
判斷共線性問題之標準為,若VIF值≥10,則認為自變數間存有共線性問題。
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
fit.vif<-lm(as.numeric(education)~age+income, data=Testdata) #擬合線性迴歸
vif(fit.vif) #計算變異數膨脹因數
→根據執行結果:2個自變數的VIF都<10,表示自變數之間不存在嚴重共線性問題,滿足適用條件5「自變數之間無多重共線性」。
(六)模型擬合
##查看變數係數##
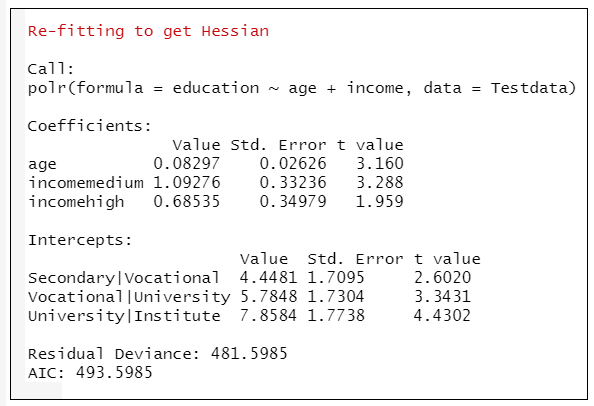
summary(fit) #模型詳細結果
→根據執行結果:顯示模型的詳細資訊。
Coefficients部分列出了截距和自變數的Value (非標準化係數)、Std. Error (標準誤差)、統計量t值。
##計算新模型中變數係數的95%CI##
confint(fit)
→根據執行結果:顯示模型中各變數係數的95%CI。
##對迴歸係數進行檢驗得出P值##
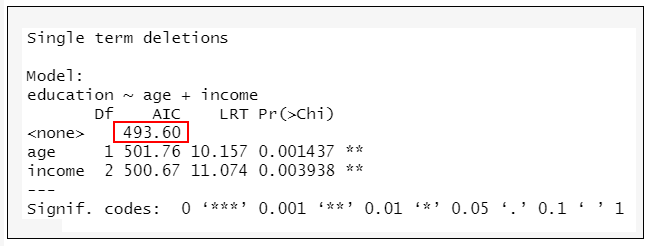
drop1(fit,test=”Chi”)
→根據執行結果:得知模型的AIC=493.60。
##計算新模型中的參數##
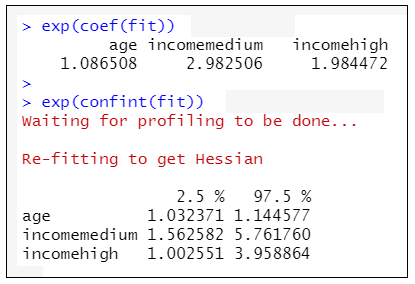
exp(coef(fit)) # 計算OR值
exp(confint(fit)) # 計算OR值的95%CI
→根據執行結果:分別得知如下:
「年齡」每增加一歲,則「教育程度」提升一個等級的機率是原來的1.087倍(95%CI:1.032~1.145);
「中收入」水準者的「教育程度」提升一個等級的機率是「低收入」水準者的2.983倍(95%CI:1.563~5.762);
「高收入」水準者的「教育程度」提升一個等級的機率是「低收入」水準者的1.984倍(95%CI:1.003~3.959)。
##模型整體檢驗##
##建立零模型(僅包含截距)
fit0<-polr(Education~1,data=Testdata)
##模型比較##
anova(fit,fit0)
→根據執行結果:得知X2=24.110,P<0.001,所建立的模型(age+income)具有顯著的差異。
四、結論
綜合以上分析,我們可以推論「年齡」和「收入」與「教育程度」之間是有顯著關係的。
以上便是有序羅吉斯迴歸分析的R語言操作,若您覺得有幫助的話,再請幫我們留個好評,謝謝您的觀看,我們下次見。






封面圖-500x383.png)

封面圖-500x383.png)
