T檢定主要用於檢定某一樣本統計量是否與總體參數相等,在實際應用中,最常見的有三種方法:獨立樣本t檢定、成對樣本t檢定和單一樣本t檢定。本篇文章主要介紹成對樣本t檢定- R語言的操作,細節如下所述。
#補充:如何選定檢定統計量
拿到資料時得先判斷裡頭是否有母體資料,以及可以取得的樣本數大小。
接著再判斷使用哪種檢定統計量:
Z檢定:
- 在母體的標準差已知,樣本數低於30以下。
- 在母體的標準差已知,樣本數超過30以上。
- 在母體的標準差未知,樣本數超過30以上。
t檢定:
- 在母體的標準差未知,樣本數低於30以下。
一、適用條件
使用成對樣本t檢定需要滿足六個條件:
條件1:變數為連續變數。
條件2:變數為相依性(資料之間彼此相關)。
條件3:變數可分為兩組。
條件4:變數沒有離群值。
#補充:Outlier(異常值或離群值):超過最小值(Q3+1.5 IQR)或最大值(Q1-1.5 IQR)的數值。
條件5:兩組變數的差值為常態分配或輕微的偏態(圖一)。
條件6:兩組變數之間存在相關性。
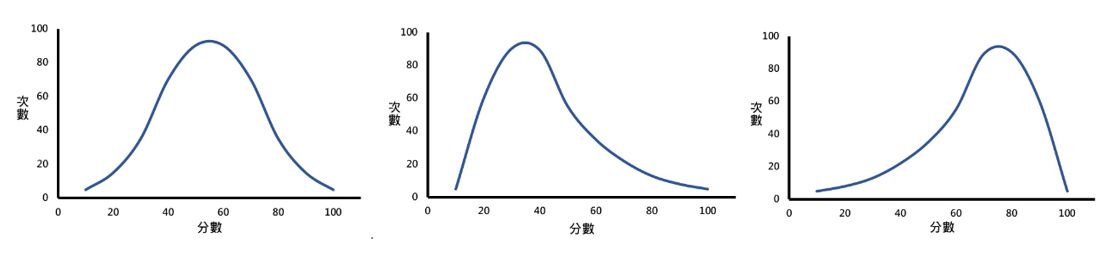
圖1 常態分配、偏態分配(正偏態、負偏態)
二、成對樣本t檢定
(1) 計算公式
成對樣本t檢定(Paired-Sample t Test)是適用於相依樣本,最常用在相依樣本下的重複量測設計,也就是同一個樣本,前後量測二次,例如:一群數學資優班學生,在入學前與入學一年後智力測驗分數是否有差異。其檢定的統計量為:

公式來源 : 蕭文龍(2016),《統計分析入門與應用:SPSS中文版+SmartPLS 3 (PLS_SEM)》,台北:碁峯資訊
(2) 假設檢定
虛無假設(Null hypothesis)→ H0:u1=u2 無顯著差異
對立假設(alternative hypothesis)→ H1:u1≠u2 有顯著差異
三、R語言操作範例
(一) 範例介紹
一群數學資優班學生,在入學前與入學一年後智力測驗分數是否有差異?
研究假設如下:
虛無假設→ H0:uD =0 即入學前/後對智力測驗分數的結果無影響;
對立假設→ H1:uD >0 即入學前/後對智力測驗分數的結果有影響。
α = 0.05
(二) 資料匯入
pairdata<-read.csv(“score-3.csv”,header=T)
# read.csv ():將資料匯入到指定的變數,也就是pairdata
View(pairdata)
# View():瀏覽資料內容
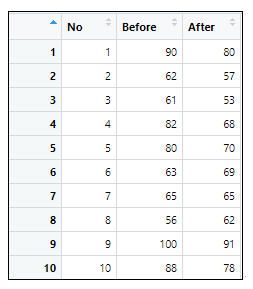
=>根據執行結果:在資料集中共有3個變數和21個觀察資料,3個變數分別為資優生的編號(No)、入學前的分數(Before)、入學一年後的分數(After)。
(三) 適用條件判定
1. 本範例的智力測驗分數為連續變數,滿足適用條件1「變數為連續變數」。
2. 本範例的智力測驗分數均是對同一批資優生測試來的,因此變數互為相依性,滿足適用條件2「變數為相依性」。
3. 本範例分為入學前和入學一年後兩組,滿足適用條件3「變數可分為2組」。
4. 離群值檢測
這裡的檢測方式採用箱型圖,來判別資料內是否存在離群值。
#補充:箱型圖(Box plot)
主要是用來顯示數據分佈情況。其組成要素為最小值、第一四分位數、中位數、第三四分位數以及最大值。
箱型圖能夠顯示出離群值(outlier),離群值也叫做異常值,通過箱型圖能夠很容易識別出資料中的異常值。
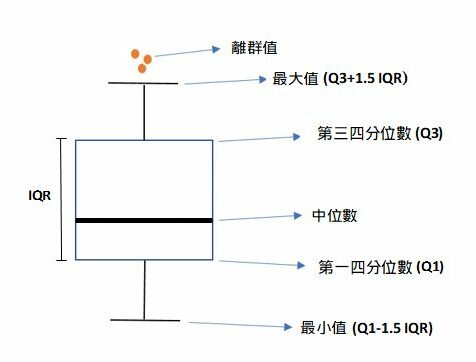
圖2 箱型圖
(1) 查看最大值和最小值
summary(pairdata$Before) #Before的描述型統計資訊
summary(pairdata$After) #After的描述型統計資訊
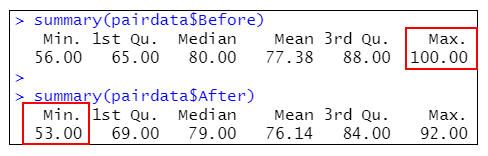
=>根據執行結果:從描述型統計資訊(Min(最小值)、1st Qu(第一四分位數)、Median(中位數)、Mean(平均值)、3rd Qu(第三四分位數)和Max(最大值))中得知,可判斷智力測驗分數均可能在53到100之間。
(2) 查看遺漏值情況
is.na(pairdata$Before) #檢查Before是否有遺漏值
is.na(pairdata$After) #檢查After是否有遺漏值

=>根據執行結果:都沒有遺漏值。
(3) 分組繪製箱型圖
par(mfrow = c(1, 2)) #設置畫1行2個圖片
boxplot(pairdata$Before, xlab = “Before”, ylab = “Score”) #繪製Before的箱型圖
boxplot(pairdata$After, xlab = “After”, ylab = “Score”) #繪製After的箱型圖
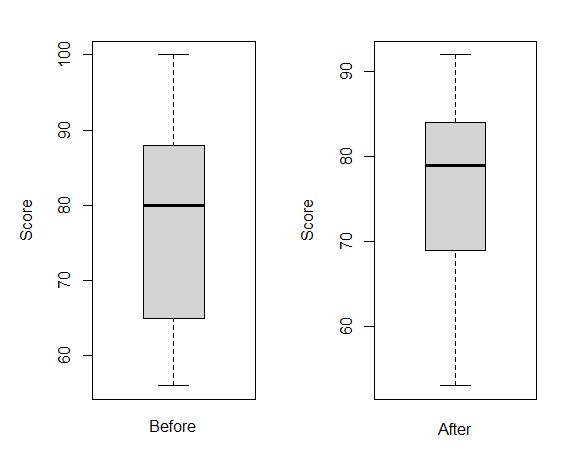
圖3 Before和After的箱型圖
=>根據執行結果:箱型圖內無顯示任何離群值,即滿足適用條件4「變數沒有離群值」。
5. 常態性檢定
這裡的檢測方式採用分位圖(Q-Q圖)和Shapiro-Wilk檢定來做是否為常態分配。
#補充:分位圖(Q-Q圖)
是一種視覺化比較兩項數據的分佈是否相同的方法。
另外,Q-Q Plot不是只有判斷「是否為直線」或者「是否為常態分配」,即使畫出來的不是直線,還是能看出資料分配的特性。
從圖1 中可以看到Q-Q Plot在左偏與右偏分配會呈現的樣子:
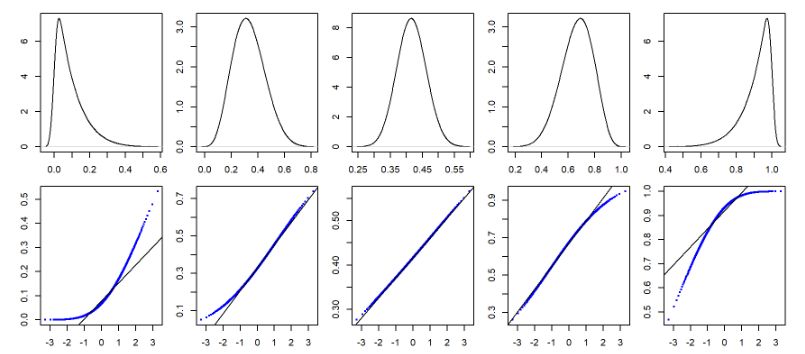
圖4 不同數值分配下的不同 Q-Q Plot(Source: Manny Gimond)
(1) 分組繪製Q-Q圖:
d <- pairdata$Before – pairdata$After #計算兩組間差值
qqnorm(d) #繪製Q-Q圖
qqline(d) #增加趨勢線
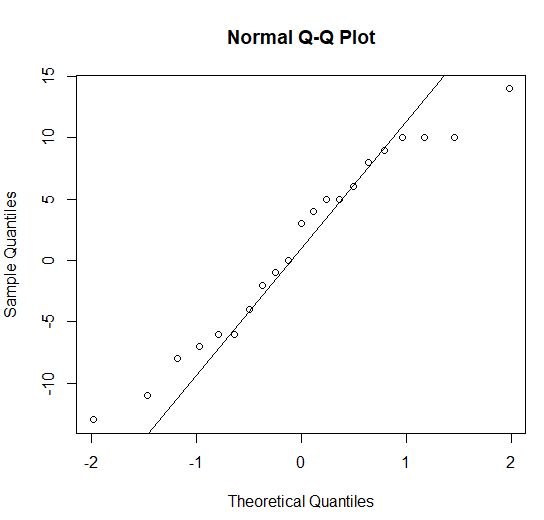
圖5 分組的Q-Q圖
=>根據執行結果:資料點基本上都圍繞對角線分佈,表示資料呈常態分配。
#補充:使用S-W檢定的原因
要進行常態性檢定有兩種方法K-S檢定或S-W檢定,因樣本數的關係而選擇使用S-W檢定。
Kolmogorov-Smirnov(K-S)檢定:樣本數50個以上。
Shapiro-Wilk(S-W)檢定:樣本數50個以下。
(2) 分組做常態性檢定:
shapiro.test(d) # Shapiro-Wilk常態性檢定

=>根據執行結果:常態性檢定的P值為0.4278 > 0.1,表示資料呈常態分配。
結合(1)(2)的結果,表示資料滿足適用條件5「變數的差值為常態分配」。
(四) 統計描述及推斷
- 描述性分析
install.packages(“psych”) #安裝套件:psych
library(psych) #載入套件:psych
describe(pairdata$Before) #描述Before的集中和離散趨勢
describe(pairdata$After) #描述After的集中和離散趨勢

=>根據執行結果:顯示各組變數的統計量,包括:vars(第幾個變數)、n (樣本量)、mean (平均數)、sd (標準差)、median (中位數)、trimmed(截尾均值)、絕對中位差(mad)、min(最小值)、max(最大值)、range(值域)、skew(偏度)、kurtosis(峰度)和se(標準誤差平均數)。
可知入學前的分數為77.38±12.46,入學一年後的分數為76.14±11.07。
- 成對樣本T檢定
t.test(pairdata$Before, pairdata$After, paired = TRUE)
# pairdata$Before, pairdata$After代表資料組x, y
# alternative設定對立假設,可以為two.sided, less, greater三個種類,因預設為alternative=two.sided,在此省略。
# paired = 用來設定是否需要成對樣本t檢定

=>根據執行結果:t =0.72769、p-value =0.4752未達顯著水準 (P>0.01),接受虛無假設。
可知數學資優班學生,在入學前與入學一年後智力測驗分數是無顯著的差異。
(五) 相關性檢定
這裡的檢定方式採用散佈圖及Pearson相關性檢定來判別資料之間,是否有相關聯性。
#補充:散佈圖(Scatter Plot)
是表示兩個變數之間關係的圖,又稱相關圖。
依下列(A)~(F)的判斷方式,檢視是否為不相關。
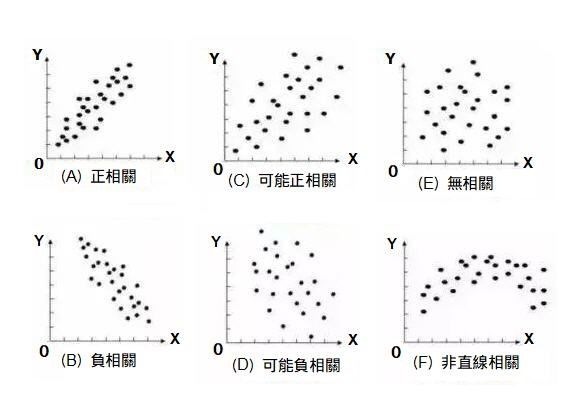
圖6 散佈圖的判斷方式
- 繪製散佈圖
plot(pairdata$Before, pairdata$After, xlab = “Before”, ylab = “After”) #繪製散佈圖
abline(lm(pairdata$After ~ pairdata$Before))
# abline():給圖形增加趨勢線
# lm(應變數(通常用Y來表示)~自變數(通常用X來表示), 資料來源):建構線性回歸模型
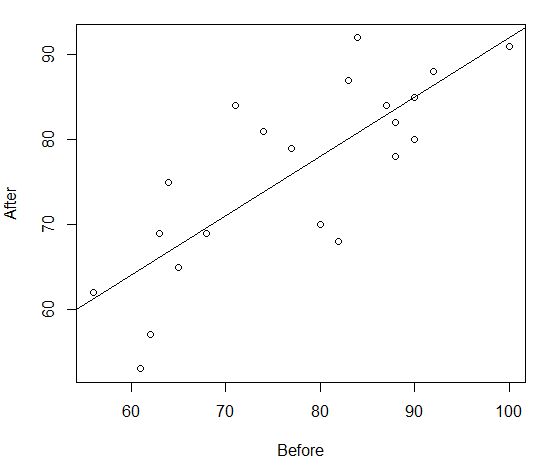
圖7 Before與After的散佈圖
=>根據執行結果:兩組之間呈線性關係(正相關)。
#補充:使用Pearson做相關性原因
處理相關性有三種檢定方式:Pearson相關性分析、Spearman等級相關性分析、Kendall’s Tau-b等級相關性分析。
以目前的條件:變數為連續變數、線性關係、無離群值、常態分配 è符合Pearson相關性分析的4個適用條件。
#補充:皮爾森相關分析的相關說明可參考:
https://www.yongxi-stat.com/pearson-correlation/
https://www.yongxi-stat.com/pearson-correlation-analysis-r/
- Pearson相關性檢定
cor.test(pairdata$Before, pairdata$After, method=”pearson”) #相關性檢定
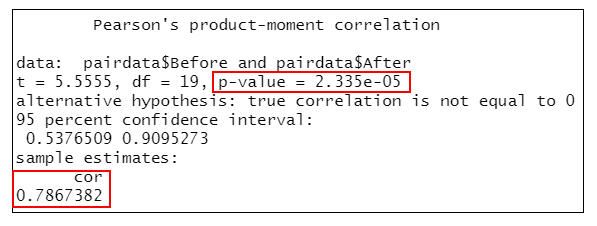
=>根據執行結果:兩組Pearson相關係數r=0.7867382 (95%CI:0.54-0.91),P<0.001,表示兩組資料之間存在相關性(高度相關)。
也就是說,入學前和入學一年後之間的分數差異變化有一致性,此結果滿足適用條件6「兩組變數之間存在相關性」。
- 結合1.和2.的結果,繪製相關性檢定結果的散佈圖
install.packages(“ggplot2”) #安裝套件:ggplot2
library(ggplot2) #載入套件:ggplot2
install.packages(“ggpubr”) #安裝套件:ggpubr
library(ggpubr) #載入套件:ggpubr
ggplot(data = pairdata, aes(x=pairdata$Before,y=pairdata$After)) +
geom_point(color=”red”) +
stat_smooth(method=”lm”,se=TRUE) +
stat_cor(data=pairdata, method = “pearson”) #繪製相關性檢定結果的散佈圖
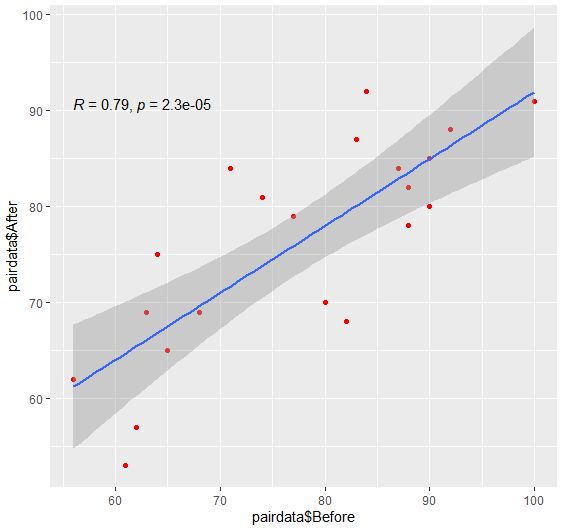
圖8 相關性檢定結果的散佈圖
=>根據執行結果:在圖中標記相關性檢定結果的散佈圖,顯示更為直觀,可以選擇性使用。
# 補充:相關性檢定是為了驗證配對資料的一致性,其可能的四種情況:
- 相關性檢定與成對樣本t檢定的P值均<0.05
表示資料在兩組間具備一致性,且有顯著的差異,而且差異的產生就是研究因素作用的結果。
- 相關性檢定的P值>0.05,成對樣本t檢定的P值<0.05
表示資料在兩組間存在差異,但平均數差異變化不一致,平均數差異可能還受其他因素的影響。
- 相關性檢定的P值<0.05,成對樣本t檢定的P值>0.05
表示資料在兩組間變化有一致性,但平均數差異不顯著,即研究因素未發揮作用。
- 相關性檢定與成對樣本t檢定的P值均>0.05
表示資料在兩組間不具備一致性,且無顯著的差異。
=>本範例為第3種情況。
四、結論
本研究採用成對樣本t檢定判斷在入學前與入學一年後智力測驗分數是否有差異。
透過箱型圖顯示兩組資料無離群值、Q-Q圖和Shapiro-Wilk檢定顯示兩組資料的差值呈現常態分配。
根據執行結果顯示,入學前與入學一年後在智力測驗分數分別為77.38±12.46和76.14±11.07,入學前平均值比入學一年後高1.24 (95%CI:-2.311~4.787),無顯著的差異(t=0.728,P>0.01)。兩組Pearson相關係數r=0.787,P<0.001;表示入學前和入學一年後之間的分數差異變化有一致性。因此,在入學前所做的智力測驗分數通常會比入學一年後的分數差不多。



封面圖-500x383.png)

