在統計學中,當考慮兩個或更多變數之間的關係時,就可能出現交互作用。
本篇文章介紹迴歸分析中的交互作用分析 – R語言的操作,細節如下所述。
一、分析目的
在實際資料分析工作中,常會出現兩個或多個變數之間存在相互作用的關係。例如研究學員年齡和教學方案等因素對多益分數的影響時,學員年齡和教學方案對依變數的影響可能存在相互作用的關係,在這種情況下就可以採用交互作用分析。
二、適用條件
由於本範例的依變數為連續型變數,考慮採用多元線性迴歸分析,並在迴歸分析中創建客戶年齡與購買手機方案的交互項以分析二者是否具有交互效應。
使用多元線性迴歸分析需要滿足以下7個條件:
條件1:樣本數量是自變數個數的5~10倍。
條件2:自變數若為連續變數,需與依變數之間具有線性關係。
條件3:觀察變數相互獨立。
條件4:觀察變數沒有異常值。
條件5:殘差為常態分配。
條件6:殘差為變異數同質性。
條件7:自變數之間無多重共線性。
三、R語言操作範例
(一)範例介紹
想瞭解客戶年齡和購買手機方案(A、B、C)與電信滿意度的關係,同時判斷客戶年齡與購買手機方案是否具有交互作用。
依變數:電信滿意度(score)。
自變數:客戶年齡(age)、購買手機方案(case)。
(二)資料匯入
scoredata <-read.csv(“123.csv”,header=T) #將資料匯入到指定的變數,也就是scoredata
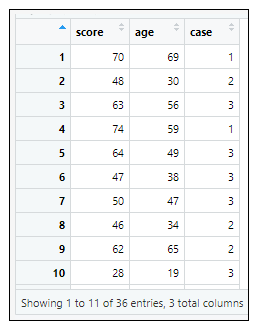
View(scoredata) #瀏覽資料內容
→根據執行結果:在資料集中共有3個變數和36個觀察資料,3個變數分別為:
電信滿意度(score)、客戶年齡(age)、購買手機方案(case;1:方案A、2:方案B、3:方案C)
##重新定義分組變數##
#將變數「case」設置為因子(factor)變數並為各類別水準 (levels)給予指定名稱。
scoredata$case <- factor(scoredata$case, labels = c(“A”, “B”, “C”))
#將購買手機方案C設置為參照組
scoredata$case <- relevel(scoredata$case, ref = “C”)
#補充:參照組(reference group)
- 一個具有K個水準的類別變項,可以轉換成K個虛擬變項,然在實際執行迴歸分析時,第K組是K-1組的數值全部為0,故實際只要K-1組,以免造成變項的多元共線性問題。
- 未經虛擬處理的水準組別,即稱為參照組。
- 參照組不一定是最後一個水準,而宜取用內容明確清楚,樣本數適中的水準作為參照組,例如「其他」就不適合做為參照組;有順序關係時,如教育水準,可以依據研究需求選擇最高等級、最低或中間等級,作為參照組。
str(scoredata) #查看數據結構
(三)含交互作用的線性迴歸
##查看模型擬合情況##
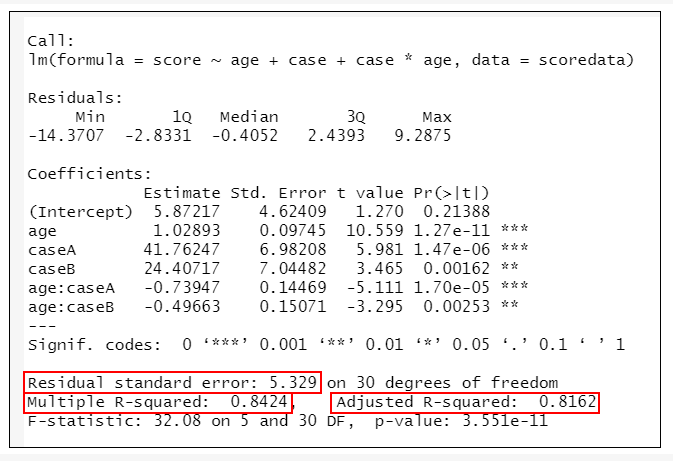
summary(lm.reg)
→根據執行結果:列出擬合後模型的各項參數。
可以看到模型的殘差標準誤差(Residual standard error, RSE)為5.329;決定係數R2=0.842,表示自變數可以解釋84.2%的依變數變異;調整後的決定係數R2=0.816,表示調整後的自變數可以解釋81.6%的依變數變異。
由分析結果可知,age與Case的交乘項的係數達顯著,表示兩者之間存在交互作用。由於係數是負向係數,由此可知相較於CaseC,在CaseA跟CaseB中年齡對滿意度的正向影響較低,我們可以由以下三個方程式解讀出來。
上述的OLS迴歸方程為:
Score = 5.872 + 1.029 x age + 41.762 x case_A + 24.407 x case_B – 0.739 x age*case_A – 0.497 x age*case_B
模型解讀:
當採用購買手機方案A時,迴歸方程為:
Score = 5.872 + 1.029 x age + 41.762– 0.739 x age = 0.289 x age +47.634
表示採用購買手機方案A時客戶的年齡每增加1歲,電信滿意度就會提高0.289分。
當採用購買手機方案B時,迴歸方程為:
Score = 5.872 + 1.029 x age + 24.407 – 0.497 x age =0.531 x age +30.279
表示採用購買手機方案B時客戶的年齡每增加1歲,電信滿意度就會提高0.531分。
當採用購買手機方案C時,迴歸方程為:
Score = 5.872 + 1.029 x age
表示採用購買手機方案C時客戶的年齡每增加1歲,電信滿意度就會提高1.028分。
由此可知,手機方案C可能更適合高齡族群,手機方案A則可能更適合年輕族群
四、結論
綜合以上,我們在執行交互作用分析時,主要目的是觀察自變數跟調節變數之間是否存在交互作用,亦即不同方案情境下自變數與依變數的關係是否會有所不同。若交互作用達顯著時,建議進一步拆解模型,這樣一來可以知道各組之間自變數跟依變數的關係,以便進一步理解交互作用背後的意涵。
五、附錄-多元迴歸適用條件判定
上述的多元迴歸分析仍需進行前提假設的檢驗,由於篇幅較長因此拉來附錄進行說明。
- 條件1判斷(樣本數量)
本範例含5個自變數,分別為客戶年齡、購買手機方案變數(2個虛擬變數)和2個交互變數,而樣本數量為36,滿足適用條件1「樣本數量是自變數個數的5~10倍」。
#補充:虛擬變數
在迴歸分析(一般線性迴歸、羅吉斯迴歸)當中,當自變數為類別變數時,我們都要先進行轉換虛擬變數(Dummy variable)的動作,以人工方式將類別變數轉化為連續變數,通常虛擬變數會設定為二元變數0或1。
- 條件2判斷(線性關係判斷)
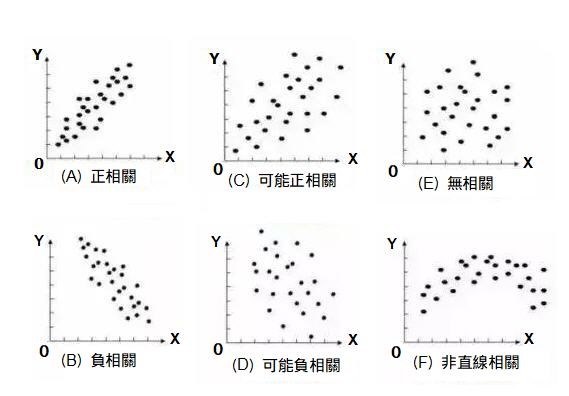
這裡的檢測方式採用散佈圖,用來判別資料之間,是否有相關聯性。
#補充:散佈圖(Scatter Plot)
是表示兩個變數之間關係的圖,又稱相關圖。
依下列(A)~(F)的判斷方式,檢視是否為不相關。
圖1. 散佈圖的判斷方式
##線性關係判斷##
install.packages(“ggplot2”) #安裝套件:ggplot2
library(ggplot2) #載入套件:ggplot2
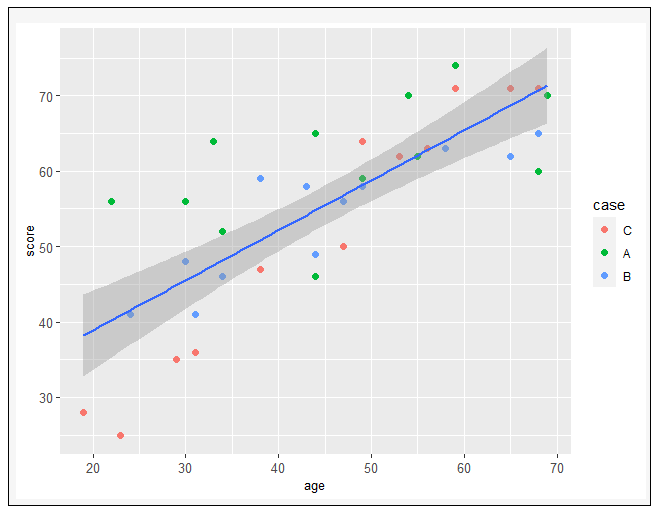
## 繪製客戶年齡與電信滿意度的散佈圖,其中客戶年齡與電信滿意度皆為連續變數。
ggplot(scoredata,aes(x=age,y=score))+
geom_point(size=2,aes(color=case))+
stat_smooth(method=”lm”,se=TRUE)+
theme(axis.title.x=element_text(size=10), axis.title.y=element_text(size=10))+
theme(axis.text.x =element_text(size=10), axis.text.y=element_text(size=10))
→根據執行結果:客戶年齡與電信滿意度的關係呈線性相關(正相關)。
表示資料滿足適用條件2「自變數與依變數之間具有線性關係」。
- 條件3判斷(獨立性判斷)
Durbin-Watson檢定:
通常用來檢測迴歸分析中的殘差項是否存在自我相關,Durbin-Watson檢定值分佈在0~4之間,越接近2,觀測值相互獨立的可能性越大。需要注意的是,判斷觀測值是否獨立,主要取決於研究設計和資料收集階段的品質控制,Durbin-Watson檢驗最好用於輔助判斷。
##獨立性判斷##
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
durbinWatsonTest(lm(score~age+case+case*age, data=scoredata))
→根據執行結果:顯示DW Statistic為2.005,P=0.962>0.05,說明觀測值之間不存在互相影響的情況,滿足適用條件3「觀察變數相互獨立」。
- 條件4判斷(異常值檢測)
庫克距離(Cook’s Distance)用來判斷強影響點是否為依變數的異常值點。
一般認為當D<0.5時不是異常值點,當D>0.5時認為是異常值點。
##計算cook距離 ##
lm.reg<-lm(score~age+case+case*age, data=scoredata) #擬合迴歸分析
cook<-cooks.distance(lm.reg) #計算Cook距離
max(cook) #顯示最大Cook距離
→根據執行結果:顯示最大庫克距離D為0.154<0.5,表示資料不存在異常值。滿足適用條件4「觀察變數沒有異常值」。
- 條件5判斷(殘差的常態性檢定)
這裡的檢測方式採用Shapiro-Wilk檢定來做是否為常態分配。
#補充:使用S-W檢定的原因
要進行常態性檢定有兩種方法K-S檢定或S-W檢定,因樣本數的關係而選擇使用S-W檢定。
Kolmogorov-Smirnov(K-S)檢定:樣本數50個以上。
Shapiro-Wilk(S-W)檢定:樣本數50個以下。
lm.reg<-lm(score~age+case+case*age,data=scoredata)
shapiro.test(lm.reg$residuals)
→根據執行結果:顯示 P=0.4824>0.05,表示殘差服從常態性分配。
表示資料滿足適用條件5「殘差為常態分配」。
- 條件6判斷(殘差的變異數同質性檢定)
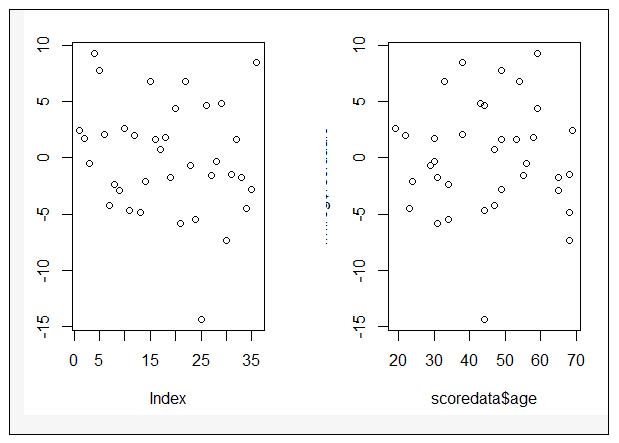
##殘差圖##
par(mfrow=c(1,2),pin = c(2,3)) #2行1列分布
plot(lm.reg$residuals)
plot(scoredata$age,lm.reg$residuals)
→根據執行結果:預測值和各變數值的殘差分佈較為均勻,並未出現特殊的分佈形式(如漏斗或者扇形),表示殘差符合變異數同質性,滿足適用條件6「殘差為變異數同質性」。
- 條件7判斷(共線性診斷)
含有交互作用的迴歸分析,通常會有多重共線性問題,因此需要對多重共線性問題進行觀察,並根據情況對資料進行調整分析。
變異數膨脹因數(Variance Inflation Factor,VIF):
為預防迴歸模型存在共線性問題,可以使用VIF來判斷解釋變數間是否存在高度多重共線性。
判斷共線性問題之標準為,若VIF值≥10,則認為自變數間存有共線性問題。
##共線性診斷##
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
lm.reg<-lm(score~age+case+case*age,data=scoredata)
vif(lm.reg) #計算變異數膨脹因數
→根據執行結果:3個自變數的VIF都<10,表示自變數之間不存在嚴重共線性問題。滿足適用條件7「自變數之間無多重共線性」。
#補充:【多元共線性之解決方法-以調節效果為例】
以上便是迴歸分析中的交互作用分析- R語言操作,若您覺得有幫助的話,再請幫我們留個好評,謝謝您的觀看,我們下次見。
在統計學中,當考慮兩個或更多變數之間的關係時,就可能出現交互作用。
本篇文章介紹迴歸分析中的交互作用分析 – R語言的操作,細節如下所述。
一、分析目的
在實際資料分析工作中,常會出現兩個或多個變數之間存在相互作用的關係。例如研究學員年齡和教學方案等因素對多益分數的影響時,學員年齡和教學方案對依變數的影響可能存在相互作用的關係,在這種情況下就可以採用交互作用分析。
二、適用條件
由於本範例的依變數為連續型變數,考慮採用多元線性迴歸分析,並在迴歸分析中創建客戶年齡與購買手機方案的交互項以分析二者是否具有交互效應。
使用多元線性迴歸分析需要滿足以下7個條件:
條件1:樣本數量是自變數個數的5~10倍。
條件2:自變數若為連續變數,需與依變數之間具有線性關係。
條件3:觀察變數相互獨立。
條件4:觀察變數沒有異常值。
條件5:殘差為常態分配。
條件6:殘差為變異數同質性。
條件7:自變數之間無多重共線性。
三、R語言操作範例
(一)範例介紹
想瞭解客戶年齡和購買手機方案(A、B、C)與電信滿意度的關係,同時判斷客戶年齡與購買手機方案是否具有交互作用。
依變數:電信滿意度(score)。
自變數:客戶年齡(age)、購買手機方案(case)。
(二)資料匯入
scoredata <-read.csv(“123.csv”,header=T) #將資料匯入到指定的變數,也就是scoredata
View(scoredata) #瀏覽資料內容
→根據執行結果:在資料集中共有3個變數和36個觀察資料,3個變數分別為:
電信滿意度(score)、客戶年齡(age)、購買手機方案(case;1:方案A、2:方案B、3:方案C)
##重新定義分組變數##
#將變數「case」設置為因子(factor)變數並為各類別水準 (levels)給予指定名稱。
scoredata$case <- factor(scoredata$case, labels = c(“A”, “B”, “C”))
#將購買手機方案C設置為參照組
scoredata$case <- relevel(scoredata$case, ref = “C”)
#補充:參照組(reference group)
- 一個具有K個水準的類別變項,可以轉換成K個虛擬變項,然在實際執行迴歸分析時,第K組是K-1組的數值全部為0,故實際只要K-1組,以免造成變項的多元共線性問題。
- 未經虛擬處理的水準組別,即稱為參照組。
- 參照組不一定是最後一個水準,而宜取用內容明確清楚,樣本數適中的水準作為參照組,例如「其他」就不適合做為參照組;有順序關係時,如教育水準,可以依據研究需求選擇最高等級、最低或中間等級,作為參照組。
str(scoredata) #查看數據結構
(三)含交互作用的線性迴歸
##查看模型擬合情況##
summary(lm.reg)
→根據執行結果:列出擬合後模型的各項參數。
可以看到模型的殘差標準誤差(Residual standard error, RSE)為5.329;決定係數R2=0.842,表示自變數可以解釋84.2%的依變數變異;調整後的決定係數R2=0.816,表示調整後的自變數可以解釋81.6%的依變數變異。
由分析結果可知,age與Case的交乘項的係數達顯著,表示兩者之間存在交互作用。由於係數是負向係數,由此可知相較於CaseC,在CaseA跟CaseB中年齡對滿意度的正向影響較低,我們可以由以下三個方程式解讀出來。
上述的OLS迴歸方程為:
Score = 5.872 + 1.029 x age + 41.762 x case_A + 24.407 x case_B – 0.739 x age*case_A – 0.497 x age*case_B
模型解讀:
當採用購買手機方案A時,迴歸方程為:
Score = 5.872 + 1.029 x age + 41.762– 0.739 x age = 0.289 x age +47.634
表示採用購買手機方案A時客戶的年齡每增加1歲,電信滿意度就會提高0.289分。
當採用購買手機方案B時,迴歸方程為:
Score = 5.872 + 1.029 x age + 24.407 – 0.497 x age =0.531 x age +30.279
表示採用購買手機方案B時客戶的年齡每增加1歲,電信滿意度就會提高0.531分。
當採用購買手機方案C時,迴歸方程為:
Score = 5.872 + 1.029 x age
表示採用購買手機方案C時客戶的年齡每增加1歲,電信滿意度就會提高1.028分。
由此可知,手機方案C可能更適合高齡族群,手機方案A則可能更適合年輕族群
四、結論
綜合以上,我們在執行交互作用分析時,主要目的是觀察自變數跟調節變數之間是否存在交互作用,亦即不同方案情境下自變數與依變數的關係是否會有所不同。若交互作用達顯著時,建議進一步拆解模型,這樣一來可以知道各組之間自變數跟依變數的關係,以便進一步理解交互作用背後的意涵。
五、附錄-多元迴歸適用條件判定
上述的多元迴歸分析仍需進行前提假設的檢驗,由於篇幅較長因此拉來附錄進行說明。
- 條件1判斷(樣本數量)
本範例含5個自變數,分別為客戶年齡、購買手機方案變數(2個虛擬變數)和2個交互變數,而樣本數量為36,滿足適用條件1「樣本數量是自變數個數的5~10倍」。
#補充:虛擬變數
在迴歸分析(一般線性迴歸、羅吉斯迴歸)當中,當自變數為類別變數時,我們都要先進行轉換虛擬變數(Dummy variable)的動作,以人工方式將類別變數轉化為連續變數,通常虛擬變數會設定為二元變數0或1。
- 條件2判斷(線性關係判斷)
這裡的檢測方式採用散佈圖,用來判別資料之間,是否有相關聯性。
#補充:散佈圖(Scatter Plot)
是表示兩個變數之間關係的圖,又稱相關圖。
依下列(A)~(F)的判斷方式,檢視是否為不相關。
圖1. 散佈圖的判斷方式
##線性關係判斷##
install.packages(“ggplot2”) #安裝套件:ggplot2
library(ggplot2) #載入套件:ggplot2
## 繪製客戶年齡與電信滿意度的散佈圖,其中客戶年齡與電信滿意度皆為連續變數。
ggplot(scoredata,aes(x=age,y=score))+
geom_point(size=2,aes(color=case))+
stat_smooth(method=”lm”,se=TRUE)+
theme(axis.title.x=element_text(size=10), axis.title.y=element_text(size=10))+
theme(axis.text.x =element_text(size=10), axis.text.y=element_text(size=10))
→根據執行結果:客戶年齡與電信滿意度的關係呈線性相關(正相關)。
表示資料滿足適用條件2「自變數與依變數之間具有線性關係」。
- 條件3判斷(獨立性判斷)
Durbin-Watson檢定:
通常用來檢測迴歸分析中的殘差項是否存在自我相關,Durbin-Watson檢定值分佈在0~4之間,越接近2,觀測值相互獨立的可能性越大。需要注意的是,判斷觀測值是否獨立,主要取決於研究設計和資料收集階段的品質控制,Durbin-Watson檢驗最好用於輔助判斷。
##獨立性判斷##
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
durbinWatsonTest(lm(score~age+case+case*age, data=scoredata))
→根據執行結果:顯示DW Statistic為2.005,P=0.962>0.05,說明觀測值之間不存在互相影響的情況,滿足適用條件3「觀察變數相互獨立」。
- 條件4判斷(異常值檢測)
庫克距離(Cook’s Distance)用來判斷強影響點是否為依變數的異常值點。
一般認為當D<0.5時不是異常值點,當D>0.5時認為是異常值點。
##計算cook距離 ##
lm.reg<-lm(score~age+case+case*age, data=scoredata) #擬合迴歸分析
cook<-cooks.distance(lm.reg) #計算Cook距離
max(cook) #顯示最大Cook距離
→根據執行結果:顯示最大庫克距離D為0.154<0.5,表示資料不存在異常值。滿足適用條件4「觀察變數沒有異常值」。
- 條件5判斷(殘差的常態性檢定)
這裡的檢測方式採用Shapiro-Wilk檢定來做是否為常態分配。
#補充:使用S-W檢定的原因
要進行常態性檢定有兩種方法K-S檢定或S-W檢定,因樣本數的關係而選擇使用S-W檢定。
Kolmogorov-Smirnov(K-S)檢定:樣本數50個以上。
Shapiro-Wilk(S-W)檢定:樣本數50個以下。
lm.reg<-lm(score~age+case+case*age,data=scoredata)
shapiro.test(lm.reg$residuals)
→根據執行結果:顯示 P=0.4824>0.05,表示殘差服從常態性分配。
表示資料滿足適用條件5「殘差為常態分配」。
- 條件6判斷(殘差的變異數同質性檢定)
##殘差圖##
par(mfrow=c(1,2),pin = c(2,3)) #2行1列分布
plot(lm.reg$residuals)
plot(scoredata$age,lm.reg$residuals)
→根據執行結果:預測值和各變數值的殘差分佈較為均勻,並未出現特殊的分佈形式(如漏斗或者扇形),表示殘差符合變異數同質性,滿足適用條件6「殘差為變異數同質性」。
- 條件7判斷(共線性診斷)
含有交互作用的迴歸分析,通常會有多重共線性問題,因此需要對多重共線性問題進行觀察,並根據情況對資料進行調整分析。
變異數膨脹因數(Variance Inflation Factor,VIF):
為預防迴歸模型存在共線性問題,可以使用VIF來判斷解釋變數間是否存在高度多重共線性。
判斷共線性問題之標準為,若VIF值≥10,則認為自變數間存有共線性問題。
##共線性診斷##
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
lm.reg<-lm(score~age+case+case*age,data=scoredata)
vif(lm.reg) #計算變異數膨脹因數
→根據執行結果:3個自變數的VIF都<10,表示自變數之間不存在嚴重共線性問題。滿足適用條件7「自變數之間無多重共線性」。
#補充:【多元共線性之解決方法-以調節效果為例】https://www.yongxi-stat.com/multicollinearity/
以上便是迴歸分析中的交互作用分析- R語言操作,若您覺得有幫助的話,再請幫我們留個好評,謝謝您的觀看,我們下次見。






封面圖-500x383.png)
封面圖-500x383.png)

