一、抽樣誤差定義與公式
近期我們常常可以看到新聞中有提到抽樣誤差(Margin of error, MOE)這個名詞,抽樣誤差可以視為問卷調查中因為抽樣所導致調查結果的不確定性(The “margin of error” is a common summary of sampling error that quantifies uncertainty about a survey result) (Stokes & Belin, 2004)。
在計算抽樣誤差時,一般我們會將α設為0.05時(此時常態分配的Z檢定值為1.96),且受訪者民眾投票意向(P)預設為50%時,95%信賴區間的抽樣誤差可以透過以下公式計算:
在上述的公式中我們可以發現,在未加權的簡單隨機抽樣調查中,樣本數N會直接影響抽樣誤差的大小,此時我們代入N=1067進去計算,MOE=![]() =0.03,就是我們常見的3%了。此外,隨著調查樣本變多,抽樣誤差的數值也就會越小。
=0.03,就是我們常見的3%了。此外,隨著調查樣本變多,抽樣誤差的數值也就會越小。
二、兩組候選人民調相比的計算方式
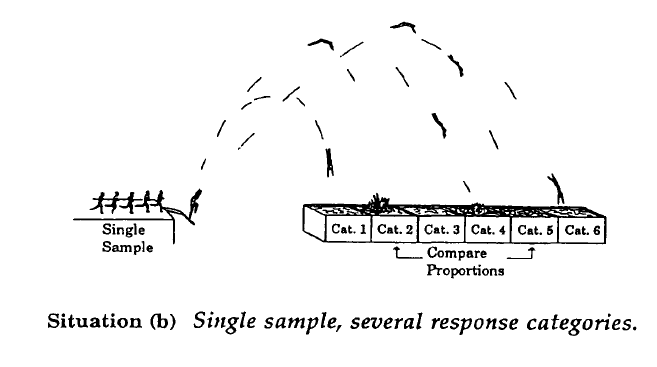
如果我們今天要針對同一份問卷調查中,比較兩組候選人的民調數值(如下圖1),則單純的使用3%當作標準會有一點不夠精確。
圖1 針對多組回答的單次樣本調查
根據Wild & Seber (1993)在Comparing two proportions from the same survey 一文中提出的建議,在我們沒有原始資料的情況下,如果僅就有限資訊要去比較兩個機率值間的差異,可採用以下步驟。假設對第一題為候選人A的支持度為![]() ,第二題候選人B的支持度為
,第二題候選人B的支持度為![]()
![]()
![]()
(二)採用的變異數評估公式應為![]()
![]()
(三)假設檢定的z公式如下
我們實際套用一筆數據來做範例說明,假設針對同一群人進行調查,結果發現![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
此外,抽樣調查其實還應考慮加權效果等其他因素的影響,詳細完整的抽樣調查仍須考量樣本加權等其他細節,本文僅就差異檢定的部分進行公式說明。此外,由於參考文獻年代較久,有些內文公式原作者可能有些許筆誤,若讀者有實際去閱讀本文的參考文獻仍需多加注意。
Reference
Stokes, L., & Belin, T. (2004). What is a Margin of Error. What is a Survey, 63-67. Retrieved from https://web.archive.org/web/20130312125540/http://www.amstat.org/sections/srms/pamphlet.pdf
Wild, C. J., & Seber, G. A. F. (1993). Comparing two proportions from the same survey. The American Statistician, 47(3), 178-181.


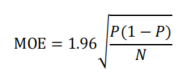
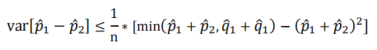
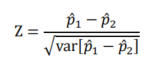

封面圖-500x383.png)

