當變數不滿足Pearson相關性分析的適用條件時，就可以採用另一種相關性分析方法——Spearman等級相關性分析。

＃補充：Spearman等級相關性分析又被稱為斯皮爾曼等級相關係數、Spearman相關係數。

一、適用條件

使用斯皮爾曼等級相關係數，需要滿足以下條件：

變數類型為：①兩個連續變數，②兩個等級變數，③一個等級變數和一個連續變數。

其中當變數類型為連續變數時，變數為非線性關係、非常態分配、或變數分佈類型未知。

二、斯皮爾曼等級相關係數

(一) 計算公式

若任一個變數裡沒有相同的等級或僅有1組或2組的相同等級（也就是平手的情況）存在時，計算斯皮爾曼等級相關係數的公式如下：

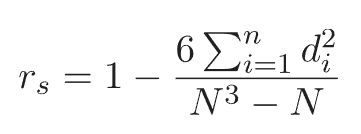
其中， di 指第 i 個配對等級的差值，也就是第 i 個第1個變數的等級減去第 i 個第2個變數的等級；N為樣本總個數（配對等級的總組數）。

若任一個變數裡有多組的相同等級存在，或只要有相同等級存在時，則可使用下面的公式：

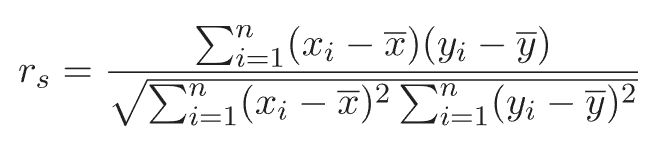
其中， 分別指第 i 個第1個變數和第2個變數的數值， 分別指第1個變數和第2個變數的平均值，

為配對的兩變數離差值的交叉乘積和。

(二) 假說檢定

虛無假說(Null hypothesis)→ H0：ρ=0 兩變數之間無顯著相關

對立假說(alternative hypothesis)→ H1：ρ≠0 兩變數之間有顯著相關

三、Ｒ語言操作範例

(一) 資料匯入

CPS85<-read.csv(“CPS85.csv”,header=T)

# read.csv ()：將資料匯入到指定的變數，也就是CPS85

View(CPS85)

# View()：瀏覽資料內容

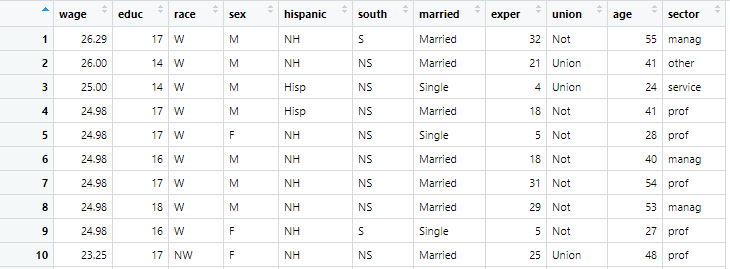
資料是使用1985年當前人口調查的資料來研究薪水和工作經驗之間的關係。

其中wage為薪水、exper為工作經驗

attach(CPS85)

# attach()：可直接使用CPS85裡面的所有變數，如exper, wage。

(二) 適用條件判定

本範例薪水(wage)和工作經驗(exper)的相關性，兩變數都是連續變數，滿足適用條件「變數類型為連續變數」。

1、常態性檢測

這裡的檢測方式採用分位圖（Q-Q圖）和Shapiro-Wilk檢定來做是否為常態分配。

＃補充：分位圖（Q-Q圖）

是一種視覺化比較兩項數據的分佈是否相同的方法。

另外，Q-Q Plot不是只有判斷「是否為直線」或者「是否為常態分配」，即使畫出來的不是直線，還是能看出資料分配的特性。

從圖1 中可以看到Q-Q Plot在左偏與右偏分配會呈現的樣子：

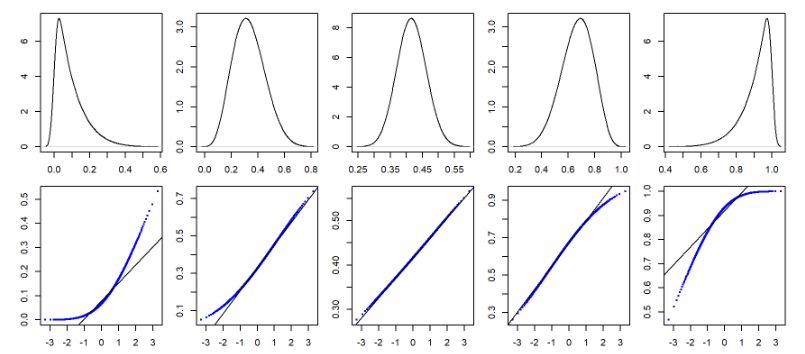
圖1 不同數值分配下的不同 Q-Q Plot（Source: Manny Gimond）

(1) 對薪水和工作經驗繪製Q-Q圖：

par(mfrow = c(1, 2))  #繪製一行2個圖片

qqnorm(exper, ylab=”year”, main=”exper”)  #繪製exper的qq圖

qqline(exper)  #增加趨勢線

qqnorm(wage, ylab=”US dollars per hour”, main=”wage”)  #繪製wage的qq圖

qqline(wage)

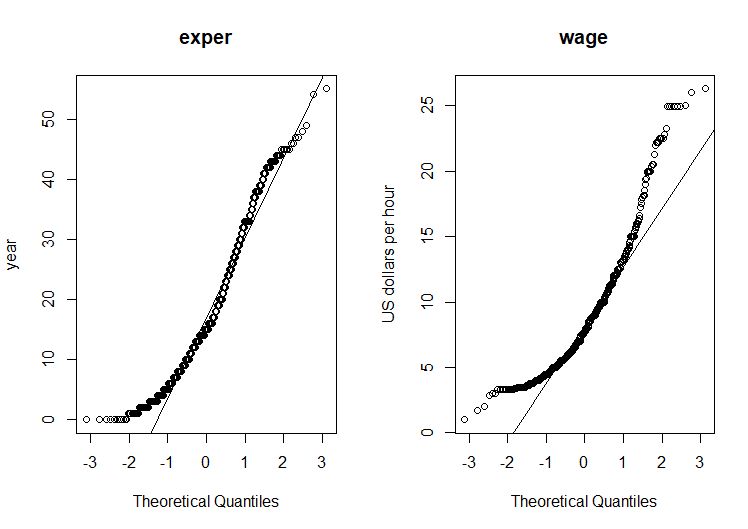
圖2 Q-Q圖（薪水和工作經驗）

根據圖2的分析結果顯示：兩個變數的散點偏離對角線分佈的較多，表示兩個變數不是常態分配。

＃補充：使用S-W檢定的原因

要進行常態性檢定有兩種方法K-S檢定或S-W檢定，因樣本數的關係而選擇使用S-W檢定。

Kolmogorov-Smirnov（K-S）檢定：樣本數50個以上。

Shapiro-Wilk（S-W）檢定：樣本數50個以下。

(2) 對薪水和工作經驗做常態性檢驗：

shapiro.test(exper)  #檢驗exper的常態性

shapiro.test(wage)  #檢驗wage的常態性

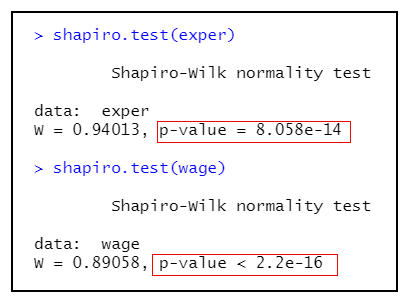
圖3 S-W檢定（薪水和工作經驗）

根據圖3的分析結果顯示：兩變數的常態性檢驗的P值均<0.001，表示不滿足常態性要求。

結合(1)(2)的結果，表示兩變數的資料滿足適用條件「連續變數為非常態分配」。

2、線性關係檢測

這裡的檢測方式採用散佈圖，用來判別資料之間，是否有相關聯性

#補充：散佈圖（Scatter Plot）

是表示兩個變數之間關係的圖，又稱相關圖。

依下列(A)~(F)的判斷方式，檢視是否為不相關。

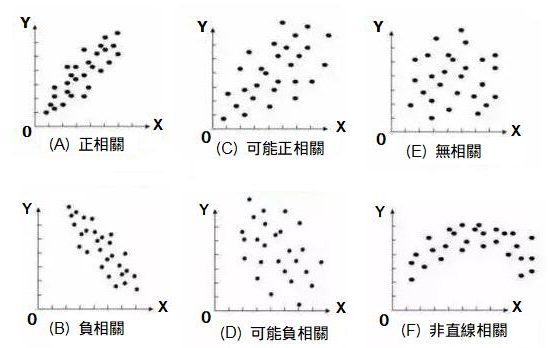
圖４ 散佈圖的判斷方式

對薪水和工作經驗繪製散佈圖：

library(ggplot2)  #載入套件

ggplot(data=CPS85, aes(x=exper, y=wage))+

　　geom_point()+stat_smooth(method=”lm”,se=TRUE)  #繪製散佈圖+趨勢線

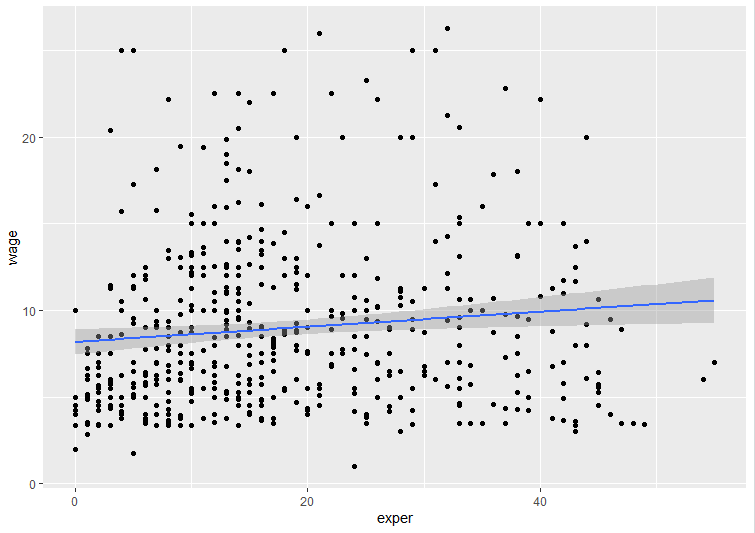
圖5 wage和exper的散佈圖

根據圖5的分析結果顯示：可見薪水和工作經驗呈非線性相關（無相關），表示資料滿足適用條件「連續變數為非線性關係」。

因此，本案例的資料滿足Spearman等級相關性分析的適用條件。

(三) Spearman等級相關性分析計算

## 相關性分析 ##

cor.test(exper, wage, alternative=”two.side”, method=”spearman”, conf.level=0.95, exact=FALSE)

# cor.test(x, y,  //檢驗的變數

　　　　　alternative = c(“two.sided”, “less”, “greater”),  

// alternative為顯著性檢定：雙尾(two.sided)、單尾(less:相關性<0,左側)(greater:相關性>0,右側)

　　　　　method = c(“pearson”, “kendall”, “spearman”),  //method為檢驗的方法

　　　　　conf.level = 0.95, exact=FALSE,…) 

//conf.level為檢驗的信賴區間的信心水準

//exact=FALSE為當資料中有重複數，透過這個得到的P值是一個近似值

根據分析結果顯示：薪水和工作經驗是有相關性。

Spearman相關係數rs=0.175，檢定統計量s=20819968，

顯著性p值=4.861e-05 < 0.001，拒絕虛無假設（ρ=0），接受對立假說（ρ≠0），兩變數間呈低度相關。

四、結論

本研究採用Spearman相關性分析對薪水和工作經驗的相關性進行了檢驗。

通過Q-Q圖和Shapiro-Wilk檢驗，表示兩變數的資料為非常態分配，通過繪製散佈圖顯示兩變數之間呈非線性關係。

Spearman相關性分析結果顯示，薪水和工作經驗之間為正相關（rs=0.175，P<0.001），工作經驗越久，民眾的薪水就會越高，但相關性程度較弱。