我們在過去執行多元迴歸時，會需要符合變異數同質性(homogeneity of variance)的基本假設，若變異數同質性有違反，則會進行加權最小平方法(WLS)的動作。

而在進行變異數同質性的檢測時，我們經常使用Breusch-Pagan test及White test兩種方式，本文主要進行White test的說明，並說明其與Breusch-Pagan test不同的地方，以及STATA的語法操作。此外，本文內容公式部分取自Wooldridge, J. M. (2015)的專書，建議有興趣的同學可以搜尋電子書查看。

一、White test計算公式

假定我們有k個自變數x，一個依變數y，組合成一個多元迴歸方程式。在進行White test 前，我們需要先計算出x₁至x_k之間的平方項及交乘項，接著再對y進行多元迴歸方程式求得殘差û，用以當作White test方程式的依變數。

在White test 的方程式中，我們根據下圖可以看到依變數為殘差平方û²，自變數為等項目。其虛無假設(H0)為所有的自變數對殘差平方的迴歸係數皆為0。

接著我們根據White test 的方程式算出，並透過LM test進行檢定，因為 (且符合卡方分配，故以LM test也可以探討是否有變異數同質性違反的情形發生。

White test的優點是有考慮更多的自變數型態進來，缺點則是增加了較多的分析項目，會使得模型較為複雜。

二、STATA操作

本次範例資料依變數為colGPA(大學成績)，自變數為hsGPA(高中成績)、ACT(成就分數)、skipped(每周翹課堂數)、PC(有無在學校使用電腦)。

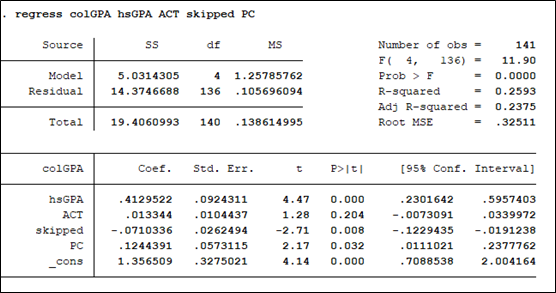
首先我們先進行多元迴歸分析，輸入語法：「regress colGPA hsGPA ACT skipped PC」後可以得到下述結果，透過這個步驟STATA程式已經算出殘差值並存在模型中。

接著我們輸入「estat imtest, white」這個語法進行White test ，就可以得出變異數同質性檢定結果。由下圖可知，其卡方值為22.79，顯著性為0.0443達顯著，表示資料存在著變異數同質性違反的問題，需要進行後續加權最小平方法(WLS)處理。

以上便是STATA操作White test的完整解說，若您覺得有幫助的話，再請幫我們留個好評，謝謝您的觀看，我們下次見。

Reference

Wooldridge, J. M. (2015). Introductory econometrics: A modern approach. Cengage learning.