我們在過去執行多元迴歸時,會需要符合變異數同質性(homogeneity of variance)的基本假設,若變異數同質性有違反,則會進行加權最小平方法(以下簡稱為WLS)或其他標準差校正的動作。以下我們將說明多元迴歸變異數同質性違反時,應進行處理的各個步驟。
一、變異數同質性違反的檢定
在之前的文章我們有提及,變異數同質性的基本假設可以透過Breusch-Pagan test (by SPSS or STATA)或White test (by SPSS or STATA)進行檢定,由於上述兩個檢定的虛無假設(H0)為變異數之間存在同質性,因此若檢定值達顯著則表示違反變異數同質性的假設。由於後續的WLS分析會根據上述檢定去進行加權值的設定,本篇文章以White test做為變異數同質性的檢定方法,以便用於後續的WLS分析。以下為White test的精簡版公式:
二、SPSS加權最小平方法的統計公式
在進行WLS之前,我們先來看一下一般的多元迴歸(OLS)方程式:
如果我們的多元迴歸方程式違反了變異數同質性,表示其變異數存在一個異質性的函數h(x),可表示如下。
由於h(x)的存在會使我們多元迴歸的估計失去有效性,因此我們需要對原本的模型進行校正,可表示如下。
由上可知,我們將多元迴歸各項皆除以加權係數,便可以解決其異質性函數的問題。根據Wooldridge(2015)的書中提及,hi可以根據我們進行同質性檢定時所使用方程式(例如:White test)的估計值(fitted value)來計算,我們在後續的分析中也會逐步說明。
三、加權最小平方法(WLS)SPSS操作過程
要使用SPSS分析WLS時,若是以White test當作變異數同質性檢定模型時,為了要符合上述有提及的檢定公式,![]() ,我們一般要經過以下六個步驟,我們接著以範例資料逐步進行分析。由於本次範例資料依變數為colGPA(大學成績),自變數為hsGPA(高中成績)、ACT(成就分數)、skipped(每周翹課堂數)、PC(有無在學校使用電腦),故下述提到的OLS便是以colGPA為依變數的多元迴歸模型。
,我們一般要經過以下六個步驟,我們接著以範例資料逐步進行分析。由於本次範例資料依變數為colGPA(大學成績),自變數為hsGPA(高中成績)、ACT(成就分數)、skipped(每周翹課堂數)、PC(有無在學校使用電腦),故下述提到的OLS便是以colGPA為依變數的多元迴歸模型。
Step 1:產出原始OLS殘差
Step 2:產出原始OLS的Y預測值(ŷ)
Step 3:計算出殘差平方
Step 4:計算出原始OLS的預測值平方(ŷ^2)
Step 5:透過變異數同質型檢定法(例如:White test)產出預測值,並取倒數後計算出加權係數(fitted value)
Step 6:進行WLS分析
(一)Step 1 & 2,根據OLS產出殘差及預測值
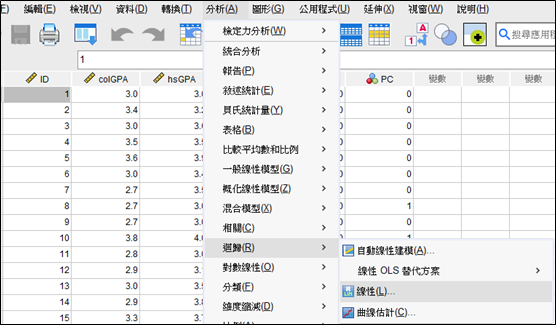
首先我們先透過迴歸分析(OLS)計算跟殘差,分析路徑為:分析->迴歸->線性
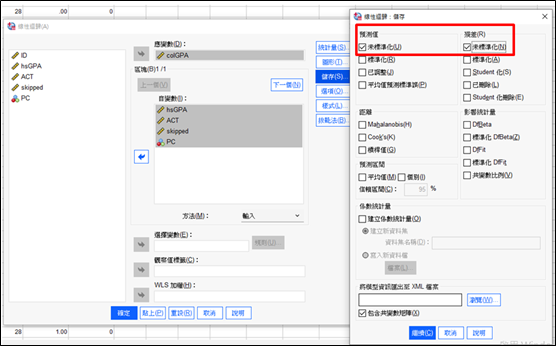
我們將colGPA放入應變數,其餘變數放入自變數,並點選「儲存」,將「預測值未標準化」、「殘差未標準化」勾選起來,便可以按確定進行分析。
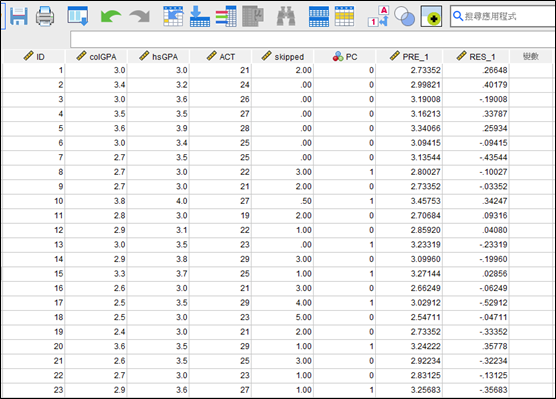
分析完後SPSS檔案會跑出PRE_1跟RES_1兩個變數,PRE_1便是ŷ,RES_1則是û。
(二)Step 3 & 4,計算殘差平方及預測值平方
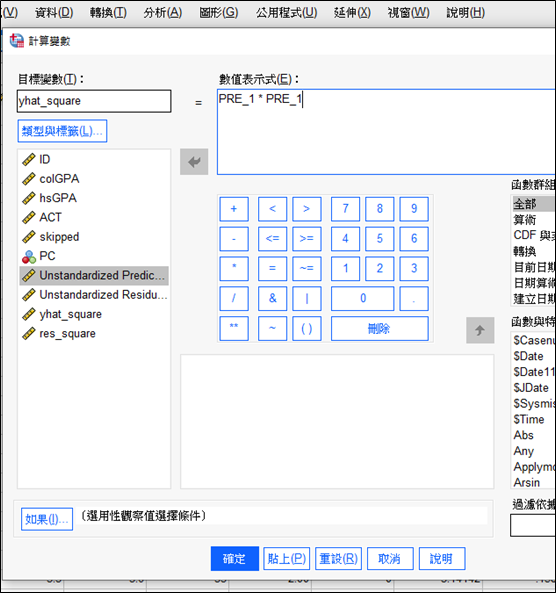
我們接著透過轉換功能中的計算變數將兩者進行平方,目標變數的名稱可以自行命名。
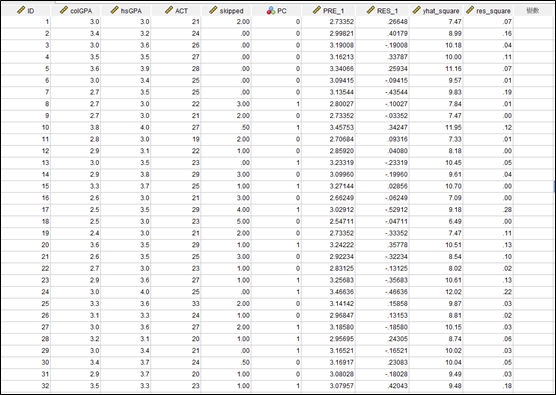
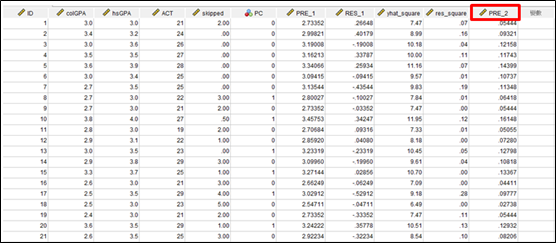
點選確定後便會得到ŷ^2(yhat_square)及û^2(res_square)兩個變數,如下圖所示。
(三)Step 5,進行White test並算出加權係數
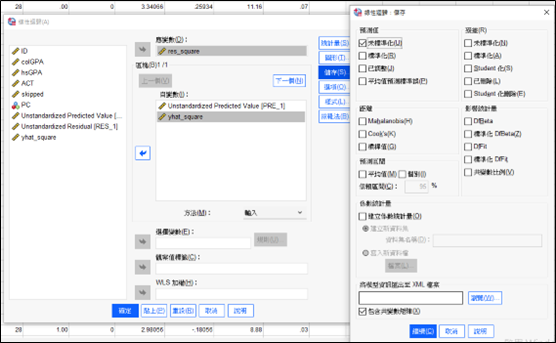
為了要進行White test我們接著把殘差平方當作應變數,及放入多元迴歸模型中,在儲存中把預測值中的「未標準化係數」勾選起來,點選確定。
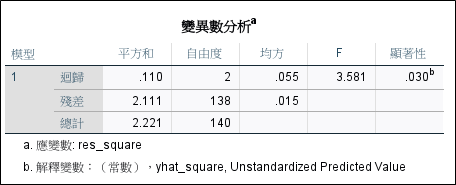
由上述White test的分析結果可知,其F值為3.581達顯著,表示違反變異數同質性的假設,需要進行加權最小平方法。
而此時我們也計算出White test這個模型的預測值,為下圖PRE_2。
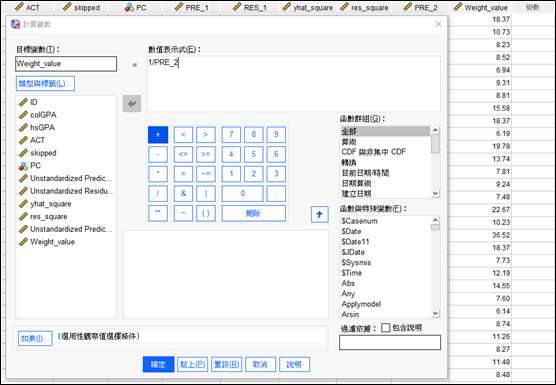
接著我們將PRE_2透過計算變數取倒數,便得到了加權係數。
(四)Step 6,進行加權最小平方法分析
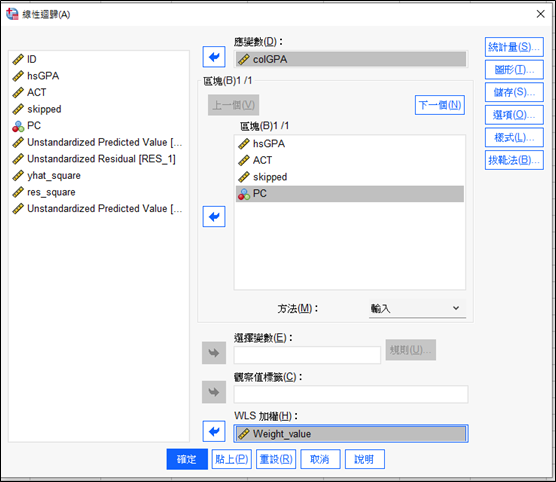
最後一個步驟,我們要將加權係數放入原本的迴歸模型中,點選「分析->迴歸->線性」,將colGPA放入應變數,其餘變數放入自變數,加權係數放入WLS加權中,點選確定即可。
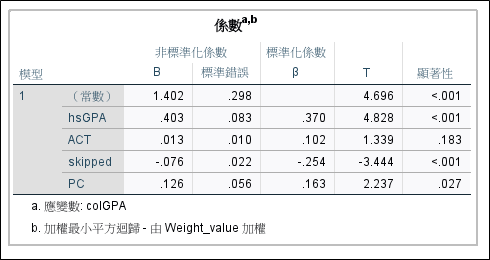
在分析結果的係數表中,我們較可以看到註解有寫到是以剛剛計算的加權係數進行調整,表示這個模型是一個WLS模型,可解決原本OLS所遇到的變異數同質性違反的問題。
以上便是SPSS操作加權最小平方法(WLS)的完整解說,若您覺得有幫助的話,再請幫我們留個好評,謝謝您的觀看,我們下次見。
Reference
Wooldridge, J. M. (2015). Introductory econometrics: A modern approach. Cengage learning.



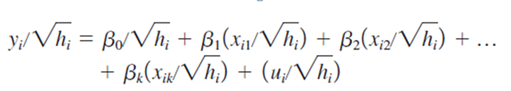

封面圖-500x383.png)

