多元迴歸分析用於探討多個預測變數及一個依變數之間的關係。
本篇文章介紹多元線性迴歸分析- R語言的操作(上),細節如下所述。
#補充:多元線性迴歸分析相關內容(SPSS)
https://www.yongxi-stat.com/multiple-regression-analysis/
一、分析目的
多元迴歸和簡單線性迴歸相同,一樣是探討自變數(x)與依變數(y)之間的關聯性,並建立出迴歸模型,藉此預測研究者感興趣的變數(y)。
有差別的部分在於,多元線性迴歸:是利用兩個以上的自變數(x)去預測一個依變數(y)。
二、適用條件
使用多元線性迴歸分析需要滿足以下7個條件:
條件1:樣本數量是自變數個數的5~10倍。
條件2:自變數若為連續變數,需與依變數之間具有線性關係。
條件3:觀察變數沒有異常值。
條件4:觀察變數相互獨立。(獨立性)
條件5:自變數之間無多重共線性。
條件6:殘差為常態分配。(常態性)
條件7:殘差為變異數同質性。(變異數同質性)
三、R語言操作範例
(一) 範例介紹
想瞭解學期總分是否受到其他因素影響。
自變數(x):性別(sex)、缺席次數(absent)、作業分數(homework)、期中考(midterm)、期末考(final)
依變數(y):學期總分(score)
(二) 資料匯入
Testdata<-read.csv(“123.csv”,header=T) #將資料匯入到指定的變數,也就是Testdata
View(Testdata) #瀏覽資料內容
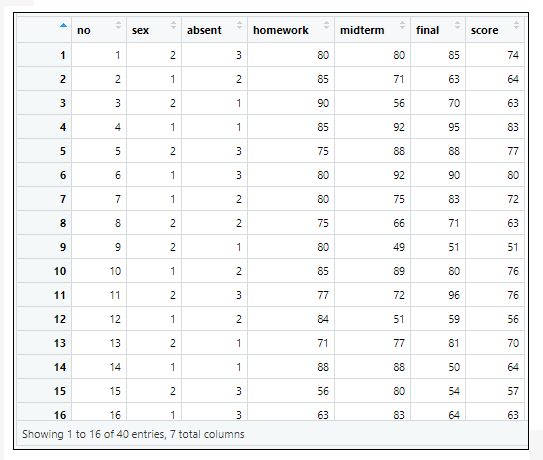
=>根據執行結果:在資料集中共有7個變數和40個觀察資料,7個變數分別為:
學生編號(no)、性別(sex)、缺席次數(absent)、作業分數(homework)、期中考(midterm)、期末考(final)、學期總分(score)。
(三) 適用條件判定
- 條件1判斷(樣本數量)
本範例含5個自變數,分別為性別、缺席次數、作業分數、期中考、期末考,而樣本數量為40,滿足適用條件1「樣本數量是自變數個數的5~10倍」。
- 條件2判斷(線性關係判斷)
這裡的檢測方式採用散佈圖,用來判別資料之間,是否有相關聯性。
#補充:散佈圖(Scatter Plot)
是表示兩個變數之間關係的圖,又稱相關圖。
依下列(A)~(F)的判斷方式,檢視是否為不相關。
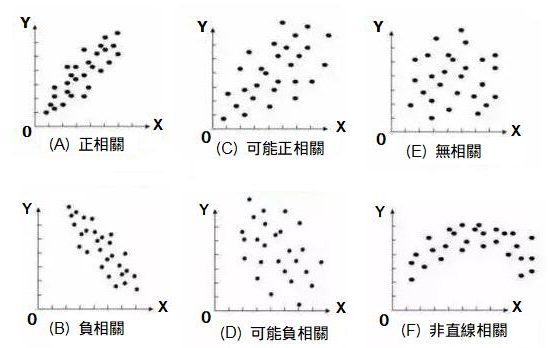
圖1. 散佈圖的判斷方式
##轉換為分組變數,並添加標籤##
Testdata$sex <-factor(Testdata$sex,labels = c(“女”,”男”))

Testdata$absent <-factor(Testdata$absent,labels = c(“低曠課”,”中曠課”,”高曠課”))

##線性關係判斷##
install.packages(“ggplot2”) #安裝套件:ggplot2
library(ggplot2) #載入套件:ggplot2
(1) 作業分數與學期總分的關係
ggplot(data=Testdata,aes(x=homework,y=score))+geom_point()+stat_smooth(method=”lm”,se=TRUE) #繪製散佈圖
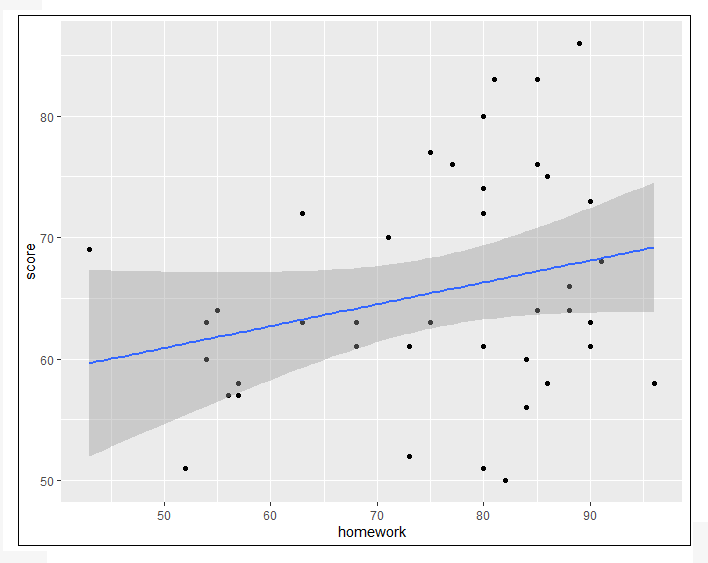
=>根據執行結果:作業分數與學期總分的關係呈線性相關(正相關)。
(2) 期中考與學期總分的關係
ggplot(data=Testdata,aes(x=midterm,y=score))+geom_point()+stat_smooth(method=”lm”,se=TRUE) #繪製散佈圖
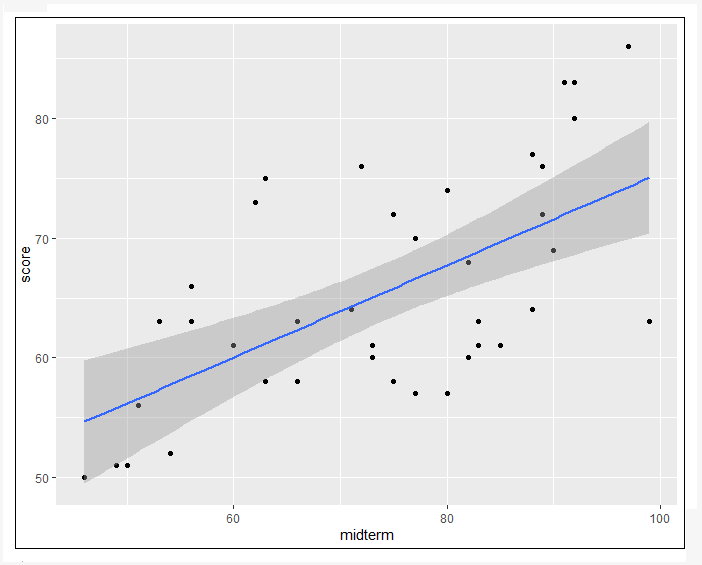
=>根據執行結果:期中考與學期總分的關係呈線性相關(正相關)。
(3) 期末考與學期總分的關係
ggplot(data=Testdata,aes(x=final,y=score))+geom_point()+stat_smooth(method=”lm”,se=TRUE) #繪製散佈圖
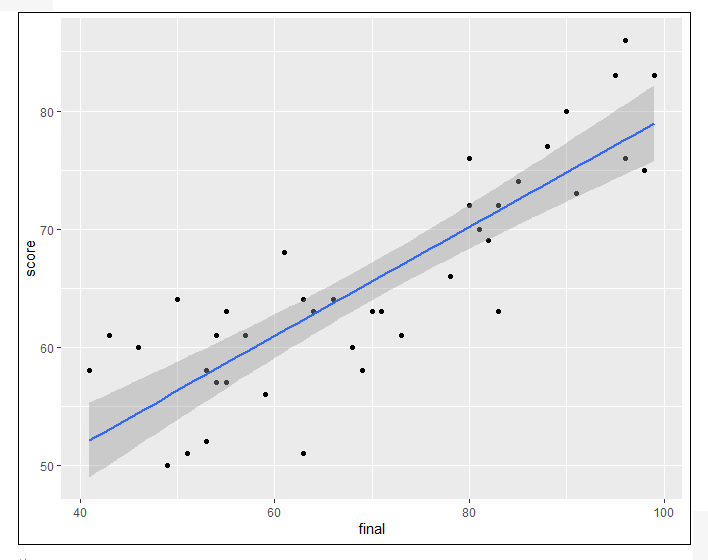
=>根據執行結果:期末考與學期總分的關係呈線性相關(正相關)。
結合(1)(2)(3)的結果,表示資料滿足適用條件2「自變數和依變數之間具有線性關係」。
- 條件3判斷(異常值檢測)
庫克距離(Cook’s Distance)用來判斷強影響點是否為依變數的異常值點。一般認為當D<0.5時不是異常值點,當D>0.5時認為是異常值點。
##計算cook距離 ##
lm.reg<-lm(score~final+midterm+homework+sex+absent,data=Testdata) #擬合迴歸分析
cook<-cooks.distance(lm.reg) #計算cook距離
cook[cooks.distance(lm.reg)>0.5] #顯示cook距離>0.5的個案編號和cook值
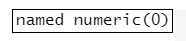
max(cook) #顯示最大cook距離
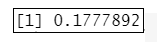
=>根據執行結果:顯示最大庫克距離D為0.178<0.5,表示資料不存在異常值。滿足適用條件3「觀察變數沒有異常值」。
- 條件4判斷(獨立性判斷)
Durbin-Watson檢定:
通常用來檢測迴歸分析中的殘差項是否存在自我相關,Durbin-Watson檢定值分佈在0~4之間,越接近2,觀測值相互獨立的可能性越大。需要注意的是,判斷觀測值是否獨立,主要取決於研究設計和資料收集階段的品質控制,Durbin-Watson檢驗最好用於輔助判斷。
##獨立性判斷##
install.packages(“car”) #安裝套件:car
library(car) #載入套件:car
durbinWatsonTest(lm(score~final+midterm+homework+sex+absent,data=Testdata)) #Durbin-Watson檢定

=>根據執行結果:顯示DW Statistic為1.816,P=0.45>0.05,說明觀測值之間不存在互相影響的情況,滿足適用條件4「觀察變數相互獨立」。
- 條件5判斷(共線性診斷)
變異數膨脹因數(Variance Inflation Factor,VIF):
為預防迴歸模型存在共線性問題,可以使用VIF來判斷解釋變數間是否存在高度多重共線性。
判斷共線性問題之標準為,若VIF值≥10,則認為自變數間存有共線性問題。
##共線性診斷##
vif(lm.reg) #計算變異數膨脹因數

=>根據執行結果:5個自變數的VIF都<10,表示自變數之間不存在嚴重共線性問題。滿足適用條件5「自變數之間無多重共線性」。
- 條件6判斷(殘差的常態性檢定)
這裡的檢測方式採用分位圖(Q-Q圖)和Shapiro-Wilk檢定來做是否為常態分配。
#補充:分位圖(Q-Q圖)
是一種視覺化比較兩項數據的分佈是否相同的方法。
另外,Q-Q Plot不是只有判斷「是否為直線」或者「是否為常態分配」,即使畫出來的不是直線,還是能看出資料分配的特性。
從圖2 中可以看到Q-Q Plot在左偏與右偏分配會呈現的樣子:
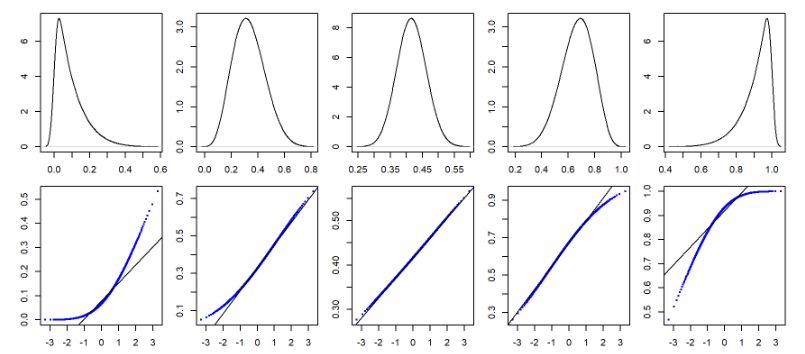
圖2 不同數值分配下的不同 Q-Q Plot(Source: Manny Gimond)
(1) 繪製Q-Q圖:
qqnorm(lm.reg$residuals) #繪製qq圖
qqline(lm.reg$residuals) #增加趨勢線
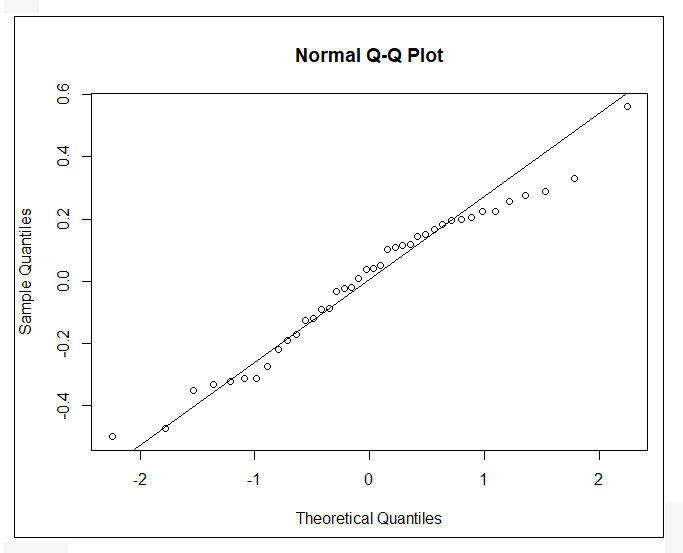
圖3 性別、缺席次數、作業分數、期中考、期末考與學期總分的Q-Q圖
=>根據執行結果:資料點基本上都圍繞對角線分佈,表示殘差符合常態性分配。
#補充:使用S-W檢定的原因
要進行常態性檢定有兩種方法K-S檢定或S-W檢定,因樣本數的關係而選擇使用S-W檢定。
Kolmogorov-Smirnov(K-S)檢定:樣本數50個以上。
Shapiro-Wilk(S-W)檢定:樣本數50個以下。
(2) 常態性檢定:
shapiro.test(lm.reg$residuals)

=>根據執行結果:顯示 P=0.3936>0.05,表示殘差符合常態性分配。
結合(1)(2)的結果,表示資料滿足適用條件6「殘差為常態分配」。
- 條件7判斷(殘差的變異數同質性檢定)
##殘差圖##
par(mfrow=c(3,2)) #2行3列分布
plot(lm.reg$residuals)
plot(Testdata$score,lm.reg$residuals)
plot(Testdata$homework,lm.reg$residuals)
plot(Testdata$midterm,lm.reg$residuals)
plot(Testdata$final,lm.reg$residuals)
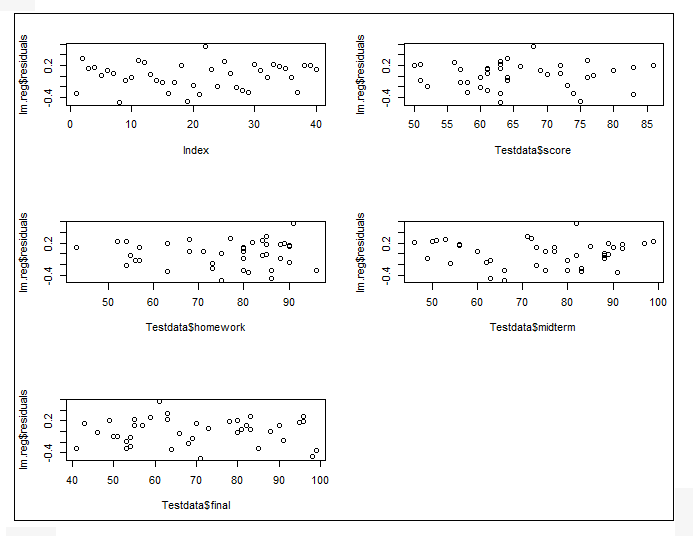
=>根據執行結果:預測值和各變數值的殘差分佈較為均勻,並未出現特殊的分佈形式(如漏斗或者扇形),表示殘差符合變異數同質性,滿足適用條件7「殘差為變異數同質性」。
#補充:此篇內容到這裡結束,請接續下篇【多元線性迴歸分析(Multiple regression analysis)- R語言操作(下) – 變數選擇+模型擬合】



封面圖-500x383.png)

